2021-06-26

物体検出

機械学習

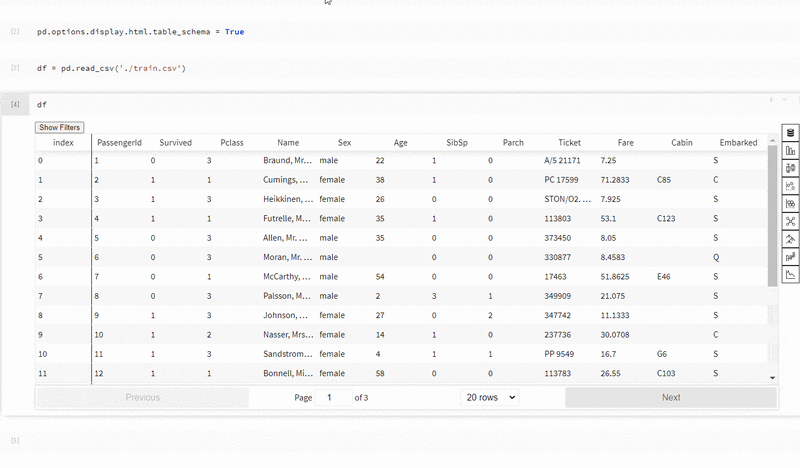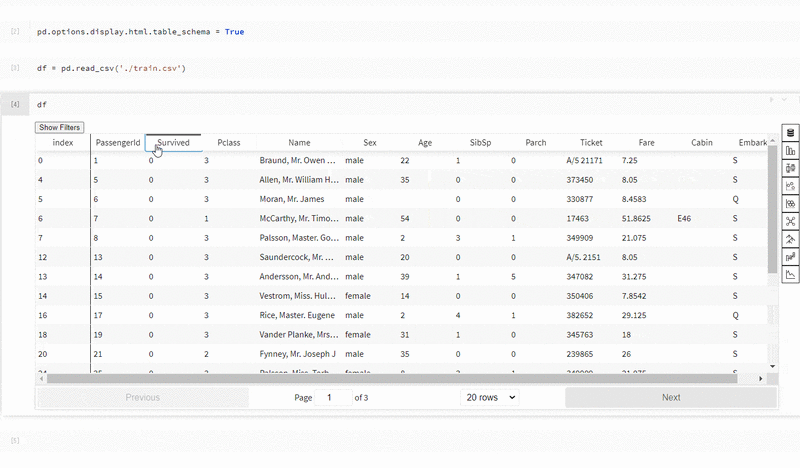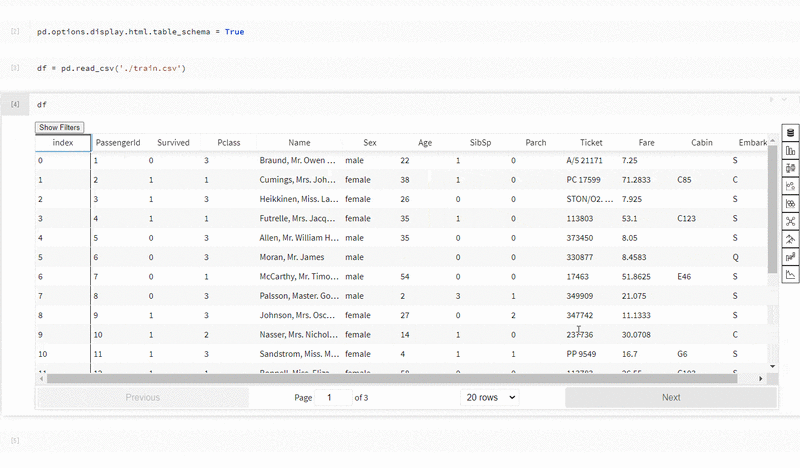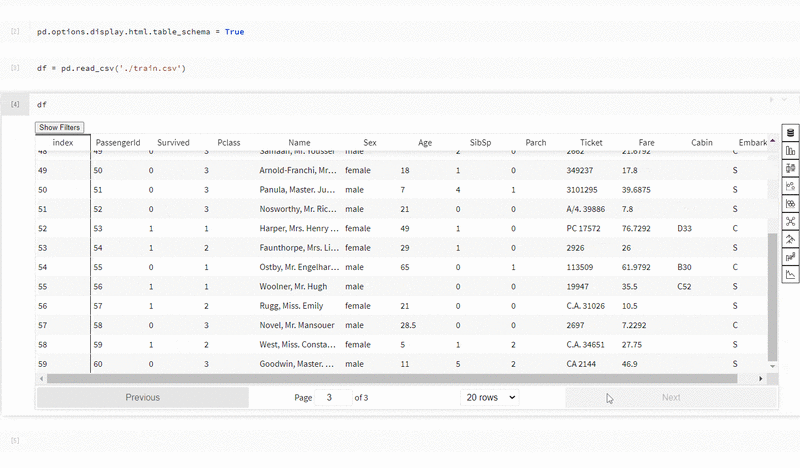
E資格の受験資格を得るために必要な日本ディープラーニング協会認定講座であるラビットチャレンジの中で出題される演習問題をベースに、E資格の深層学習パートの解説と例題をまとめました。

今回の記事では、E資格範囲の後半部分に出てくる応用的な部分をまとめていきます。

試験範囲の前半部分は以下のリンクに記載してあります。

kazukiigeta.com

RNN (Recurrent Neural Network)
LSTM
- Q4
  - 解答例
- Q5
  - 解答例
GRU (Gated Recurrent Unit)
- Q6
  - 解答例
- Q7
  - 解答例
双方向RNN
- Q8
  - 解答例
Seq2Seq
- Encoder RNN
- Decoder RNN
  - Q9
    - 解答例
  - Q10
    - 解答例
- HRED
Word2vec
Attention Mechanism
- Q11
  - 解答例
強化学習
AlphaGo
- Alpha Go (Lee)
- Alpha Go Zero
軽量化・高速化技術
応用モデル
Transformer
物体検出・セグメンテーション
Seq2seq
Transformer
最後に

RNN (Recurrent Neural Network)

RNNとは、再帰的なつながりを持つネットワークで、自然言語や時系列データなどの連続性を持つデータに対して良く用いられます。

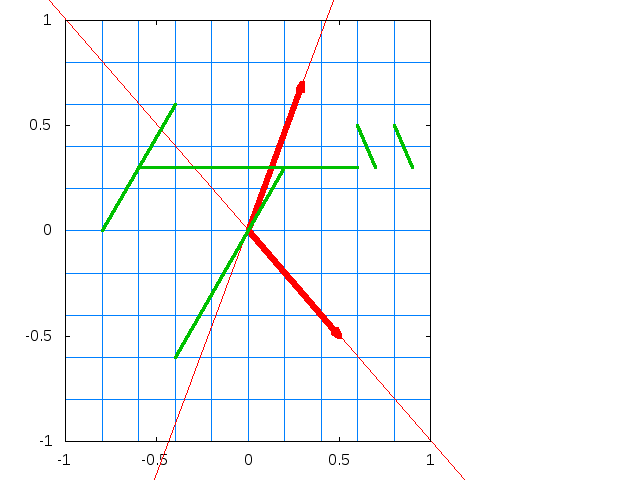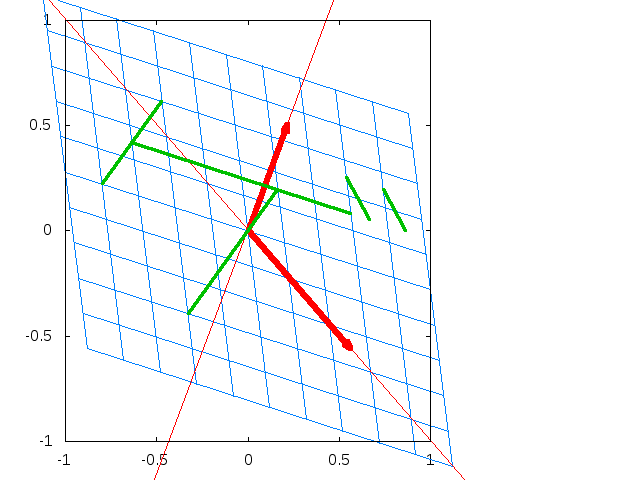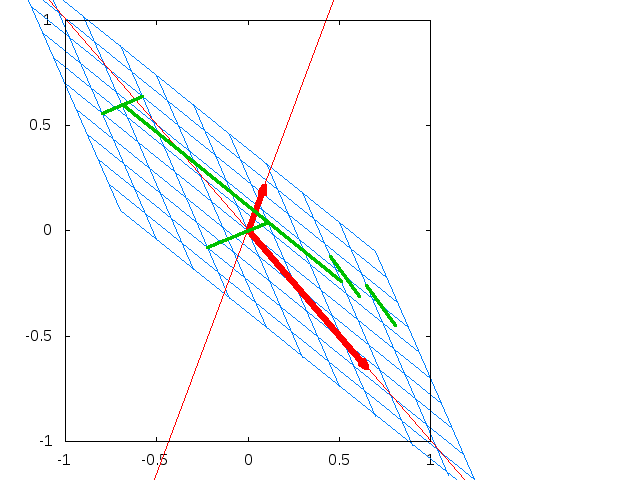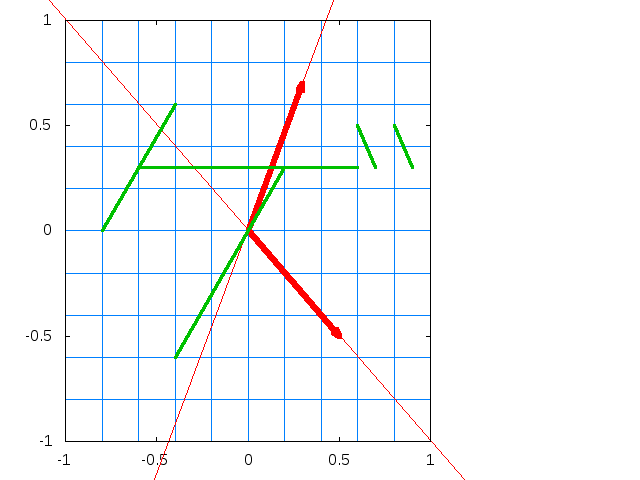
RNNのアーキテクチャは、以下の図の左側または、それを分解した右側のグラフで示されますが、どちらも同じことを意味しています。

上のグラフを数学的に表すと以下の様になります。

RNNの再帰部分の数学的表記（ベクトル）

$\displaystyle{\boldsymbol{z}_0}$ はランダムに決定された値が使われます。入力 $\displaystyle{\boldsymbol{x}}$ と[重み行列 $\displaystyle{W_{(in)}}$ との内積が活性化関数 $\displaystyle{f}$ を通して $\displaystyle{\boldsymbol{z}_t}$ となります。

$\displaystyle{ \boldsymbol{u}_t = W_{(in)}\boldsymbol{x} + W\boldsymbol{z}_{t-1} + \boldsymbol{b} \\ \boldsymbol{z}_t = f(\boldsymbol{u}_t) \\ \boldsymbol{v}_t = W_{(out)}\boldsymbol{z}_t + \boldsymbol{c}\\ \boldsymbol{y}_t = g(\boldsymbol{v}_t) \\ }$

RNNの再帰部分のPython表記

変数や関数の定義が足りていないため以下のコード単体で実行できるものではありませんが、上述の数学表記は以下の様にPythonで実装することが出来ます。

※バイアスは[w_0}]として重み行列に含まれているものとします。

u[:, t+1] = np.dot(x, W_in) + np.dot(z[:, t].reshape(1, -1), W)
z[:, t+1]  = sigmoid(u[:, t+1])
y[:, t] = sigmoid(np.dot(z[:, t+1].reshape(1, -1), W_out)

Q1

RNNのネットワークには大きく分けて以下の3つの重みがあります。以下にそのうちの2つを示しました。残り1つの重みを説明してみてください。

入力から現在の中間層を定義する際に乗算される重み
中間層から出力層を定義する際に乗算される重み
?

解答例

回答は、中間層から次の中間層に再帰的に乗算される重みです。

Q2

以下は、RNNにおいて構文木を入力として再帰的に分全体の表現ベクトルを得るPythonスクリプトです。

ただし、_activation関数は何らかの活性化関数であり、気構造は再帰的な辞書で定義されているとします。

■に当てはまるコードを選んでみてください。

(1) W.dot(left + right)
(2) W.dot(np.concatenate([left, right])
(3) W.dot(left * right)
(4) W.dot(np.maximum(left, right))

def traverse(node):
    '''
    node: tree node, recursive dict, {left: node, right: node}
              if leaf, word embedded vector, (embed_size,)
    W: weights, global variable, (embed_size, 2*embed_size)
    b: bias, global variable, (embed_size,)
    '''
    if not isinstance(node, dict):
        v = node
    else:
        left = traverse(node['left'])
        right = traverse(node['right'])
        v = _activation(■)
    return v

解答例

答えは、(2)です。

隣接単語を表す表現ベクトル2つから1つの表現ベクトルを作るという処理は、隣接している表現ベクトルleftとrightを結合して重みを掛けることで実現されます。

def traverse(node):
    '''
    node: tree node, recursive dict, {left: node, right: node}
              if leaf, word embedded vector, (embed_size,)
    W: weights, global variable, (embed_size, 2*embed_size)
    b: bias, global variable, (embed_size,)
    '''
    if not isinstance(node, dict):
        v = node
    else:
        left = traverse(node['left'])
        right = traverse(node['right'])
        v = _activation(W.dot(np.concatenate([left, right])
    return v

BPTT (Backpropagation Through Time)

RNNの再帰的なネットワークに対して誤差逆伝播を行うための手法としてBPTTと呼ばれる方法があります。

以下のグラフにて表すことができます。

BPTTのパラメータ更新

$\displaystyle{ \begin{eqnarray} W^{(in)}_{t+1} &=& W^{(in)}_{t} - \epsilon \frac{\partial E}{\partial W^{(in)}} \nonumber \\ &=& W^{(in)}_{t} - \epsilon \frac{\partial E}{\partial \boldsymbol{u}_t} \frac{\partial \boldsymbol{u}_t}{\partial W_{(in)}} \nonumber \\ &=& W^{(in)}_{t} - \epsilon \sum_{i=0}^{T_t} \frac{\partial E}{\partial \boldsymbol{u}_{t-i}} \boldsymbol{x}_{t-i} \nonumber \\ \end{eqnarray} }$

$\displaystyle{ \begin{eqnarray} W^{(out)}_{t+1} &=& W^{(in)}_{t} - \epsilon \frac{\partial E}{\partial W^{(out)}} \nonumber \\ &=& W^{(out)}_{t} - \epsilon \frac{\partial E}{\partial \boldsymbol{v}_t} \frac{\partial \boldsymbol{v}_t}{\partial W_{(out)}} \nonumber \\ &=& W^{(out)}_{t} - \epsilon \frac{\partial E}{\partial \boldsymbol{v}_{t}} \boldsymbol{z}_{t} \nonumber \\ \end{eqnarray} }$

$\displaystyle{ \begin{eqnarray} W_{t+1} &=& W_{t} - \epsilon \frac{\partial E}{\partial W} \nonumber \\ &=& W_{t} - \epsilon \frac{\partial E}{\partial \boldsymbol{u}_t} \frac{\partial \boldsymbol{u}_t}{\partial W} \nonumber \\ &=& W_{t} - \epsilon \sum_{i=0}^{T_t} \frac{\partial E}{\partial \boldsymbol{u}_{t-i}} \boldsymbol{z}_{t-1-i} \nonumber \\ \end{eqnarray} }$

BPTTの再帰部分

$\displaystyle{\boldsymbol{u}_t}$ には時間的に前の計算グラフからの誤差逆伝播が伝わってきます。 $\displaystyle{\boldsymbol{u}_t}$ と $\displaystyle{\boldsymbol{u}_{t-1}}$ の関係性は以下の通りです。

$\displaystyle{ \begin{eqnarray} \boldsymbol{u}_t &=& W_{(in)}\boldsymbol{x} + W\boldsymbol{z}_{t-1} + \boldsymbol{b} \nonumber \\ &=& W_{(in)}\boldsymbol{x} + W f(\boldsymbol{u}_{t-1}) + \boldsymbol{b} \ \ \ \because \ \boldsymbol{z}_t = f(\boldsymbol{u}_t) \nonumber \\ \end{eqnarray} }$

$\displaystyle{ \frac{\partial \boldsymbol{u}_t}{\partial \boldsymbol{u}_{t-1}} = W f'(\boldsymbol{u}_{t-1}) }$

したがって、RNNの再帰部分は以下の様にして前の時系列からの次の時系列への勾配の更新が行われます。

$\displaystyle{ \frac{\partial E}{\partial \boldsymbol{u}_{t-1}} = \frac{\partial E}{\partial \boldsymbol{u}_{t}} \frac{\partial \boldsymbol{u}_{t}}{\partial \boldsymbol{u}_{t-1}} = \frac{\partial E}{\partial \boldsymbol{u}_{t}} \left\{ \frac{\partial \boldsymbol{u}_{t}}{\partial \boldsymbol{z}_{t-1}} \frac{\partial \boldsymbol{z}_{t-1}}{\partial \boldsymbol{u}_{t-1}} \right\} = \frac{\partial E}{\partial \boldsymbol{u}_{t}} \left\{ W f'(\boldsymbol{u}_{t-1}) \right\} }$

Q3

下図の $\displaystyle{\boldsymbol{y}_1}$ を、 $\displaystyle{\boldsymbol{x}_1, \, \boldsymbol{z}_0, \, \boldsymbol{z}_1, \, W_{(in)}, \, W, \, W_{(out)}}$ をを用いて数式で表してみてください。

なお、中間層の出力にはシグモイド関数 $\displaystyle{g(\boldsymbol{x})}$ を作用させてください。

解答例

解答は以下の通りです。

バイアスには適当な文字を割り当てています。

$\displaystyle{ \boldsymbol{y}_1 = g(W_{(out)} \cdot g(W_{(out)} \boldsymbol{x}_1 + W \boldsymbol{z}_0 + \boldsymbol{b}) + \boldsymbol{c}) }$

LSTM

RNNの課題として、BPTTにて時系列を遡るほど勾配が消失していくために長い時系列の学習が困難という点があります。

逆に、学習率に大きな値を使用したり、活性化関数に恒等関数を使ったりした場合には時系列を遡るほど勾配が指数関数的に大きくなり損失関数の最小値がいつまでも収束しないという勾配爆発が起きることもあります。

Q4

勾配爆発を防ぐための手法として、勾配クリッピングと呼ばれる手法があります。勾配のノルムが閾値を超えた際に勾配のノルムを閾値に正規化するという仕組みになっています。

以下の勾配クリッピングの関数において、■に当てはまるコードを以下の4つから選んでみてください。

(1) grad * rate
(2) grad / norm
(3) grad / threshold
(4) np.maximum(grad, threshold)

def gradient_clipping(grad, threshold):
    '''
    grad: gradient
    '''
    norm = np.linalg.norm(grad)
    rate = threshold / norm
    if rate < 1:
        return ■
    return grad

解答例

答えは(1)です。

ノルムがthresholdを超えた際に、ノルムがthresholdぴったしになるようにベクトルの要素を小さくしてあげるという処理になっています。

def gradient_clipping(grad, threshold):
    '''
    grad: gradient
    '''
    norm = np.linalg.norm(grad)
    rate = threshold / norm
    if rate < 1:
        return grad * rate
    return grad

CEC (Constant Error Crousel)

LSTMでは、RNNの学習機能と前の情報を記憶する機能を分離し、記憶する機能をCECに保持させています。

時系列的な勾配が1となれば、つまり、以下の式を満たすことができれば勾配消失および勾配爆発を防ぐことが出来ます。

$\displaystyle{ \frac{\partial E}{\partial \boldsymbol{u}_{t-1}} = \frac{\partial E}{\partial \boldsymbol{u}_{t}} \left\{ W f'(\boldsymbol{u}_{t-1}) \right\} = 1 }$

※ 上式で示す時系列的な重み更新については、BPTTの再帰部分で説明済みです。

CECが持っていない学習機能は、入力ゲートと出力ゲートという部分が持っています。

入力ゲート

CECに記憶させる方法を学習します。

今回の入力値と前回の出力値をもとに今回の入力を記憶させる方法を決めます。 LSTMのアーキテクチャでいう所の $\displaystyle{W_i}$ は、今回の入力をどれくらい使うか、 $\displaystyle{U_i}$ は、前回の出力をどれくらい使うかということを学習していきます。

出力ゲート

CECに記憶を出力させる方法を学習します。

入力ゲートと同様、今回の入力値と前回の出力値をもとに今回の入力を記憶させる方法を決めます。 LSTMのアーキテクチャでいう所の $\displaystyle{W_o}$ は、今回の入力をどれくらい使うか、 $\displaystyle{U_o}$ は、前回の出力をどれくらい使うかということを学習していきます。

ここまでで、学習しながら過去の情報を記憶できるようになりましたが、このままではいつまでも古い情報が削除されずに保管され続けます。

そこで古い情報の削除を行うのが忘却ゲートです。

Q5

以下のコードは、LSTMの順伝播を行うPythonスクリプトです。ただし、_sigmoid関数は要素ごとにシグモイド関数を作用させる関数とします。

■に当てはまるコードを以下の4つから選んでみてください。

(1) output_gate * a + forget_gate * c
(2) forget_gate * a + output_gate * c
(3) input_gate * a + forget_gate * c
(4) forget_gate * a + input_gate * c

def lstm(x, prev_h, prev_c, W, U, b):
    '''
    x: inputs, (batch_size, input_size)
    prev_h: outputs at the previous time step, (batch_size, state_size)
    W: upward weights, (4*state_size, input_size)
    U: lateral weights, (4*state_size, state_size)
    b: bias, (4*state_size,)
    '''
    lstm_in = _activation(x.dot(W.T) + prev_h.dot(U.T) + b)
    a, i, f, o = np.hsplit(lstm_in, 4)

    a = np.tanh(a)
    input_gate = _sigmoid(i)
    forget_gate = _sigmoid(f)
    output_gate = _sigmoid(o)

    c = ■
    h = output_gate * np.tanh(c)
    return c, h

解答例

答えは、(3)です。

新しいセルの状態は、セルへの計算された入力に入力ゲートを掛け合わせたものと、1ステップ前のセルの状態に忘却ゲートを掛け合わせたものの和として表現されます。

def lstm(x, prev_h, prev_c, W, U, b):
    '''
    x: inputs, (batch_size, input_size)
    prev_h: outputs at the previous time step, (batch_size, state_size)
    W: upward weights, (4*state_size, input_size)
    U: lateral weights, (4*state_size, state_size)
    b: bias, (4*state_size,)
    '''
    lstm_in = _activation(x.dot(W.T) + prev_h.dot(U.T) + b)
    a, i, f, o = np.hsplit(lstm_in, 4)

    a = np.tanh(a)
    input_gate = _sigmoid(i)
    forget_gate = _sigmoid(f)
    output_gate = _sigmoid(o)

    c = input_gate * a + forget_gate * c
    h = output_gate * np.tanh(c)
    return c, h

覗き穴結合入力ゲートや出力ゲートと違って、CEC自身の値を重み行列を介して伝播可能にした構造です。

GRU (Gated Recurrent Unit)

LSTMでは、パラメータ数が多すぎて計算負荷が大きいという問題を解決するために生まれた手法です。

Q6

LSTM全体の課題について、簡潔に答えてみてください。

解答例

LSTMは、パラメータ数が多く計算コストが大きいことが課題になっています。

Q7

以下のコードは、GRUの順伝播を行うPythonスクリプトです。ただし、_sigmoid関数は要素ごとにシグモイド関数を作用させる関数とします。

■に当てはまるコードを以下の4つから選んでみてください。

(1) z.dot(h_bar)
(2) (1-z).dot(h_bar)
(3) z.dot(h).dot(h_bar)
(4) z.dot(h_bar) + (1-z).dot(h)

def gru(x, h, W_r, U_r, W_z, U_z, W, U):
    '''
    x: inputs, (batch_size, input_size)
    h: outputs at the previous time step, (batch_size, state_size)
    W_r, U_r: weights for reset gate
    W_z, U_z: weights for update gate
    U, W: weights for new state
    '''
    r = _sigmoid(x.dot(W_r.T) + h.dot(U_r.T))
    z = _sigmoid(x.dot(W_z.T) + h.dot(U_z.T))

    h_bar = np.tanh(x.dot(W.T) + (r * h).dot(U.T))
    h_new = ■
    return h_new

解答例

答えは(4)です。

新しい中間状態は1ステップ前の中間表現と計算された中間表現の線形和で表現されます。

def gru(x, h, W_r, U_r, W_z, U_z, W, U):
    '''
    x: inputs, (batch_size, input_size)
    h: outputs at the previous time step, (batch_size, state_size)
    W_r, U_r: weights for reset gate
    W_z, U_z: weights for update gate
    U, W: weights for new state
    '''
    r = _sigmoid(x.dot(W_r.T) + h.dot(U_r.T))
    z = _sigmoid(x.dot(W_z.T) + h.dot(U_z.T))

    h_bar = np.tanh(x.dot(W.T) + (r * h).dot(U.T))
    h_new = z.dot(h_bar) + (1-z).dot(h)
    return h_new

双方向RNN

過去のステップの情報だけでなく、未来のステップの情報を加味することで精度を向上させたRNNモデルのことです。

機械翻訳などで用いられています。

Q8

以下のコードは、双方向RNNの順伝播を行うPythonスクリプトです。ただし、_rnn関数はRNNの順伝播を表し中間層の系列を返す関数であるとします。

■に当てはまるコードを以下の4つから選んでみてください。

(1) h_f + h_b[::-1]
(2) h_f * h_b[::-1]
(3) np.concatenate(h_f, h_b[::-1]], axis=0)
(4) np.concatenate(h_f, h_b[::-1]], axis=1)

def bidirectional_rnn_net(xs, W_f, U_f, W_b, U_b, V):
    '''
    W_f, U_f: forward RNN weights, (hidden_size, input_size)
    W_b, U_b: backward RNN weights, (hidden_size, input_size)
    V: output weights, (output_size, 2*hidden_size)
    '''
    xs_f = np.zeros_like(xs)
    xs_b = np.zeros_like(xs)
    for i, x in enumerate(xs):
        xs_f[i] = x
        xs_b[i] = x[::-1]
    hs_f = _rnn(xs_f, W_f, U_f)
    hs_b = _rnn(xs_b, W_b, U_b)
    hs = [■ for h_f, h_b in zip(hs_f, hs_b)]
    ys = hs.dot(V.T)
    return ys

解答例

答えは(4)です。

双方向RNNでは、順方向と逆方向に伝播した時の中間層表現を結合したものが特徴量となります。

コメントに記載されたVのサイズからも横方向に結合するべきことが分かります。

def bidirectional_rnn_net(xs, W_f, U_f, W_b, U_b, V):
    '''
    W_f, U_f: forward RNN weights, (hidden_size, input_size)
    W_b, U_b: backward RNN weights, (hidden_size, input_size)
    V: output weights, (output_size, 2*hidden_size)
    '''
    xs_f = np.zeros_like(xs)
    xs_b = np.zeros_like(xs)
    for i, x in enumerate(xs):
        xs_f[i] = x
        xs_b[i] = x[::-1]
    hs_f = _rnn(xs_f, W_f, U_f)
    hs_b = _rnn(xs_b, W_b, U_b)
    hs = [np.concatenate([h_f, h_b[::-1]], axis=1) for h_f, h_b in zip(hs_f, hs_b)]
    ys = hs.dot(V.T)
    return ys

Seq2Seq

Seq2Seqとは、Encoder-Decoderモデルの1種であり、日本語文などの入力をベクトル表現にエンコードし、そのベクトル表現を英語文などの出力へデコードするといった働きをします。

過去の文の出力から文脈を意識して次の文を出力するといったことはできません。

Encoder RNN

Seq2SeqのEncoder部分は大きく分けて以下の2つの機能からなります。

Taking

文章を単語などのトークンに分割し、それぞれのトークンにIDを割り当てOne-hotベクトルへ変換します。

このとき、1万のトークンに分割されていれば、One-hotベクトルの要素数は1万となります。

Embedding

One-hotベクトルの各要素を、トークンそれぞれの意味が似ている要素を集約していくような考え方でRNNによって分散表現ベクトルを得ます。

このとき、分散表現ベクトルの要素数は数百程度になっています。

Decoder RNN

RNNのデコーダ部分では、分散表現ベクトルを入力として文などの出力します。

Sampling

生成確立に基づいて、トークンをランダムに選びます。

Embedding

選んだトークンをEmbeddingしてDecoder RNNへの次の入力とすることを繰り返し、トークンを文字列へ変換します。

Q9

以下の選択肢から、seq2seqについて説明しているものを選んでみてください。

(1) 時刻に関して順方向と逆方向のRNNを構成し、それら2つの中間層表現を特徴量として利用するものである。
(2) RNNを用いたEncoder-Decoderモデルの一種であり、機械翻訳などのモデルに使われる。
(3) 構文木などの機構増に対して、隣接単語から表現ベクトル（フレーズ）を作るという演算を再帰的に行い（重みは共通）、文全体の表現ベクトルを得るニューラルネットワークである。
(4) RNNの一種であり、単純なRNNにおいて問題となる勾配消失問題をCECとゲートの概念を導入することで解決したものである。

解答例

答えは(2)です。

問題の項目は、それぞれ以下の内容に関連しています。

(1) 双方向RNN
(2) seq2seq
(3) 構文木
(4) LSTM

Q10

機械翻訳タスクにおいて、入力は複数の単語からなる文（文章）であり、それぞれの単語はone-hotベクトルで表現されています。

Encoderにおいて、それらの単語は単語埋め込み（Embedding）により特徴量に変換され、RNNによって時系列の情報を持つ特徴へエンコードされます。

以下に入力である文を時系列の情報を持つ特徴量へエンコードする関数をPythonで記載しました。ただし、_activation関数は何らかの活性化関数を表すとします。

■に当てはまるコードを選択してみてください。

(1) E.dot(w)
(2) E.T.dot(w)
(3) w.dot(E.T)
(4) E * w

def encode(words, E, W, U, b):
    '''
    words: sequence words (sentence), one-hot vectors, (n_words, vocab_size)
    E: word embedding matrix, (embed_size, vocab_size)
    W: upward weights, (hidden_size, hidden_size)
    U: lateral weights, (hidden_size, embed_size)
    b: bias, (hidden_size,)
    '''
    hidden_size = W.shape[0]
    h = np.zeros(hidden_size)
    for w in words:
        e = ■
        h = _activation(W.dot(e) + U.dot(h) + b)
    return h

解答例

答えは、(1)です。

wordsは、one-hotベクトルであるw毎に取り出され、埋め込み行列Eとの内積（単語埋め込み）により、別の特徴量へ変換されます。

def encode(words, E, W, U, b):
    '''
    words: sequence words (sentence), one-hot vectors, (n_words, vocab_size)
    E: word embedding matrix, (embed_size, vocab_size)
    W: upward weights, (hidden_size, hidden_size)
    U: lateral weights, (hidden_size, embed_size)
    b: bias, (hidden_size,)
    '''
    hidden_size = W.shape[0]
    h = np.zeros(hidden_size)
    for w in words:
        e = E.dot(w)
        h = _activation(W.dot(e) + U.dot(h) + b)
    return h

HRED

seq2seqとContext RNN合わせた手法であり、過去n-1個の文の出力から次の出力を生成します。

例：

「インコかわいいよね」
「うん」
「インコかわいいの分かる」

seq2seqでエンコーダの出力として得られる分散表現ベクトルを、さらに別のseq2seqへ渡すContext RNNによって隠れ層を過去の文脈を含むベクトルへ変換する構造になっています。

HREDの課題確率的な生成が行われないため、同じコンテキストが与えられると毎回同じ文の出力が行われます。

また、「うん」「そうだね」といった短く情報量に乏しい文を出力しがちです。

HREDに対して潜在変数にN(0, 1)を仮定したVAEの概念を追加することで、確率的な出力を行うVHREDという手法になります。

Word2vec

分散表現を得るため手法としてword2vecというものが提案されてきました。

これは、先に述べているように疎なone-hotベクトルではなく密なベクトルとして特徴表現を得ることができる手法です。

Attention Mechanism

seq2seqは、長い文への対応が難しいという課題があり、例えば文が2単語からでも100単語から成っていても、固定次元ベクトルで表現される必要がありました。

そこで、文が長くなるほどシーケンスの内部表現の次元も大きくなっていくという、Attention Mechanismの仕組みを取り入れられました。

Q11

RNNとword2vec、seq2seq、Attentionの違いを簡潔に説明してみてください。

解答例

RNN: 時系列データを処理するのに適したネットワーク
word2vec: 文の分散表現ベクトルを得る方法
seq2seq: 1つの時系列データから別の時系列データを得るネットワーク
Attention: 時系列データの中身の内部表現の関連性に重みを与える方法

強化学習

強化学習とは、長期的に報酬を最大化できるように、環境の中で行動を選択できるエージェントを作るための機械学習分野です。

以下で示すイメージの様に、方策、状態、価値という3つの要素が存在しており、エージェントは状態に合わせて価値が高くなる方策を学習していきます。

価値関数

価値関数には主に以下の2種類があり、現在は行動価値関数Qが用いられています。

ゴールまで今の方策を続けたときの報酬の予測値として値が得られます。

状態価値関数 $\displaystyle{V^\pi(s)}$ : 状態に応じて報酬を計算する
行動価値関数 $\displaystyle{Q^\pi(s, a)}$ : 状態と行動のセットに対して報酬を計算する

方策関数

方策関数 $\displaystyle{\pi(s) = a}$ : ある状態でどのような行動をとるかを確率として与える関数

方策勾配法

得られる報酬が最大となるように、方策関数のパラメータ $\displaystyle{\theta}$ を最適化する手法として、以下の方策勾配法があります。

$\displaystyle{\theta^{t+1} = \theta^t + \epsilon \nabla J(\theta)}$

$\displaystyle{\nabla J(\theta) = E_{\pi_\theta} [ \left( \nabla_\theta \log \pi_\theta(a | s) Q^\pi (s, a) \right) ]}$

ニューラルネットワークでは誤差を最小化するパラメータを求めましたが、強化学習では期待報酬を最大化するという目的で最適化を行います。

AlphaGo

Alpha Go (Lee)

Alpha Goの方策関数にはPolicyNet、価値関数にはValueNetと呼ばれるネットワークを使います。

囲碁の目は19×19の2次元であるため、両ネットワークではCNNが使われています。

PolicyNetは、次に打つべき目を確率で出力してくれます。

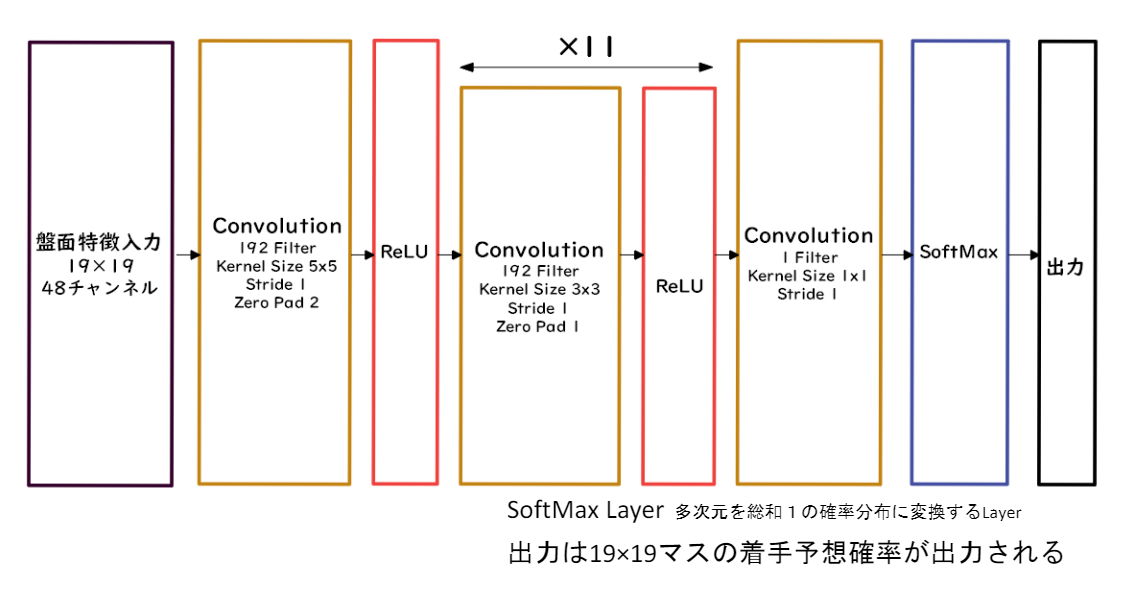
ValueNetは現局面の勝率を-1～1の間で表した値を出力してくれます。

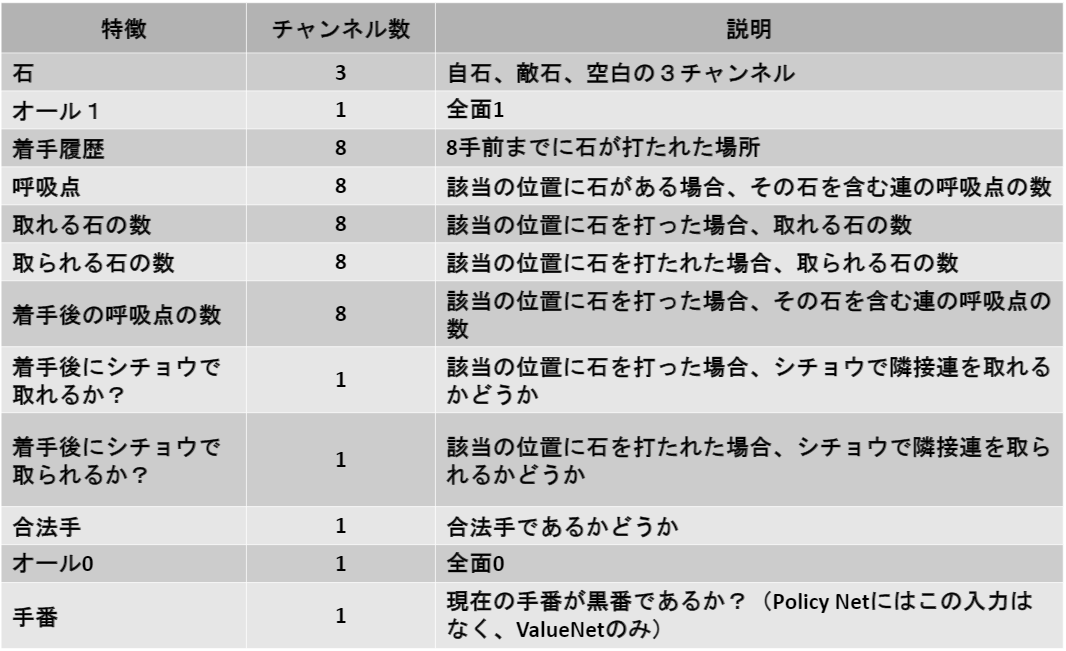
また、PolicyNetおよびValueNetへの入力はそれぞれ48チャネル、49チャネルとなっていますが、その内訳は以下の通りです。

学習ステップ

教師あり学習によるRollOutPolicyとPolicyNetの学習
強化学習によるPolicyNetの学習
強化学習によるValueNetの学習

RollOutPolicyは、ニューラルネットワークではなく線形関数であり、高速に学習を進めるために学習ステップの初期に利用されます。

Alpha Go Zero

AlphaGo (Lee)とAlpha Go Zeroに違いは以下の通りです。

教師あり学習を一切行わず、強化学習のみで作成
特徴入力からヒューリスティックな要素（人間が判断して特徴量を作成すること）を排除し、石の配置のみにした
PolicyNetとValueNetを1つのネットワークに統合した
ResidualNetを導入した
RollOutシミュレーションをなくした

ResidualNetwork

ネットワークにショートカット構造を追加することで、勾配消失・勾配爆発を抑える効果を狙っています。これにより、100層を超えるネットワークでの安定した学習を可能としました。

軽量化・高速化技術

分散深層学習

データ並列化

データが大きい際に用いられる並列化です。

複数のワーカー（端末自体またはGPUなどの計算機）を用意して、分割したデータを各ワーカに計算させる方法です。

同期型データ並列化では、以下の図のように全ワーカーの計算終了を待ち、各ワーカの計算した勾配の平均を使って親モデルのパラメータを更新します。

非同期型データ並列化では、以下の図のように各ワーカーは自分の学習が終了するとモデルをサーバにプッシュします。新たに学習を始める際にはサーバから最新のモデルをポップして学習を始めます。

性能は、多くの場合で以下の関係性となります。

速度: 非同期型 > 同期型
安定性: 非同期型 < 同期型
精度: 非同期型 < 同期型

モデル並列化

モデルが大きい場合に用いられる並列化です。モデル並列化は、多くの場合、1台の端末上の複数GPU上で実行されます。

モデルの軽量化

量子化 (Quantization)

ネットワークが大きくなると大量のパラメータが必要となり、学習や推論に多くのメモリ、GPU/CPUを必要とします。

パラメータの64bit浮動小数点を32bitなどへ精度を落とす（32bitで量子化する）ことで、メモリ使用量と演算処理のコスト削減を行います。

量子化によって、モデルの表現力は低下することになるはずと思われますが、実際には64bit（倍精度）から32bit（単精度）にしてもほとんどモデルの精度は変わらないようです。

蒸留

教師モデル
- 大きなモデルやアンサンブルされたモデルなどの予測精度が高いモデル
生徒モデル
- 教師モデルをもとに作る軽量なモデル

学習済みの教師モデルの重みは固定したまま、教師モデルの出力と生徒モデルの出力の誤差（Soft target loss）と、正解ラベルと生徒モデルの出力の誤差（Hard target loss）を使って重みを更新してきます。

プルーニング

重みが閾値以下となったニューロンを削除して再学習を行うことで、モデルの軽量化および高速化を行うことが出来ます。

応用モデル

MobileNet

軽量で高速な画像認識のモデルです。

Depthwise Separable convolutionという手法で、畳み込み演算を以下の2つに分解して順に実行することで、一般的な畳み込みに比較して大幅に計算量とパラメータを削減します。

Depthwise convolution: フィルタ数が1
Pointwise convolution: カーネルサイズが1×1

カーネルのチャネル数は、1であっても入力マップのチャネル数Cであっても計算量は同じになります。

一般的な畳み込みの計算量は、以下の図で示すところのH×W×C×K×K×Mとなります。

Depthwise convolutionの計算量は、以下の図で示すところのH×W×C×K×Kとなります。

Pointwise convolutionの計算量は、以下の図で示すところのH×W×C×Mとなります。

計算量を表にまとめます。

手法	計算量
一般的な畳み込み	H×W×C×K×K×M
Depthwise separable convolution	H×W×C×K×K + H×W×C×M

DenseNet

CNNの層が深くなるにつれて勾配消失や勾配爆発の問題により学習難しくなるという問題がありました。

この問題への対処となるResNetと似たアーキテクチャで、同じく問題対処が可能となるDenseNetというものが存在します。

DenseNetには、DenseBlockと呼ばれる部分があり、そこでは以下の図のように、出力層に前の層の入力をチャネルとして足し合わせることでチャネル数が成長率kずつ増えていきます（この例ではk=3）。

前の層の入力をチャネルとして足し合わせる部分は、以下の様にして実現されています。

上図のBatch正規化ついては、次の章Batch正規化で説明します。

DenseBlockを抜けると特徴マップのチャネル数が増えていくため、DenseBlockの次の層のConvolution層およびPooling層にて元のチャネル数までサイズを落とされます。

Batch正規化

バッチ正規化では、同一チャネルのミニバッチ内のサンプルを平均0、分散1となるよう標準化する手法です。

バッチ正規化の狙い
- 学習時間短縮
- 初期値への依存低減
- 過学習の抑制
バッチ正規化の問題
- バッチサイズが小さい条件下では、学習が収束しないことがある

Layer正規化

ハードウェア性能が低い端末での実行時の様に、バッチサイズを小さくする必要がある場合には、バッチ正規化ではなくレイヤ正規化を用いることが出来ます。

レイヤ正規化の特徴
- 結果がミニバッチサイズに依存しない
- 入力データのスケールに関してロバスト
- 重み行列のスケールやシフトに関してロバスト

Instance正規化

各サンプルの各チャネルで平均0、分散1となるよう標準化する手法です。バッチ正規化のバッチサイズが1の場合と同じ動きになります。

インスタンス正規化の特徴
- 画像コントラストの正規化に寄与
- 画像のスタイル転送やテクスチャ合成タスクなどで利用される

WaveNet

Pixel CNNという画像生成モデルを音声に応用したものです。

通常の畳み込みではなく、Dialted convolutionが適用されます。

層が深くなるにつれて、畳み込むリンクを離す
受容野を簡単に増やすことが出来る

Transformer

物体検出・セグメンテーション

物体認識タスクには以下の4つのタスクが存在します。

分類 (Classification)
物体検出 (Object detection)
意味領域分割 (Semantic segmentation)
個体領域分割 (Instance segmentation)

データセット

代表的な画像データセットについて、クラス数を横軸に、Box/画像数（1枚あたりに含まれる検出対象）を縦軸にプロットしたものを以下にプロットすることが出来ます。

クラス数が大きいデータセットには、ノートパソコンの画像に対してLaptopとNotebookといった本来統一した1ラベルを与えるべきものが複数に分かれているものも存在しています。

目的に応じて適したデータセットを選択する必要があります。

評価指標

物体検出の評価指標には、confidenceとIoU (Intersection over Union)が存在します。

confidenceはクラス分類のタスクで用いられる評価指標と同じものです。

一方、IoUは、物体位置の予測精度を評価することが出来る指標です。

Ground-Truth BBと呼ばれる物体位置の正解を示す領域に対して、Predicted BBと呼ばれる物体位置予測の精度を評価します。

Unionを分母に取っている理由は、Ground-Truth BBとPredicted BBがどちらか一方に完全に包含されている場合を考えてみると理解できます。

例えば、Predicted BBを画像いっぱいに大きく取った場合、IoC定義の分母をUnionとしていなければ正しく予測できているとはとても言えない状況なのにIoCが最大値の1を取ってしまいます。

Precision/Recallの計算

以下の条件で評価した際のPrecisionおよびRecallについて画像で示します。

入力画像1枚に車、人、犬が含まれる
confidenceの閾値=0.5, IoUの閾値=0.5

AP/mAP

RP曲線（Recall-Precision曲線）を積分することでAP（Average Precision）という単一のクラスに対する指標を算出することが出来ます。

Confidenceの大きい順に並べ、PR曲線をRecallに関する関数とみなしてPR曲線下側の面積を求めるという流れになっています。

mAP（mean Average Precision）は、複数クラスそれぞれにおいてAPを計算し、算術平均を取ったものです。

1段階検出器/2段階検出器

物体検知には、候補領域の検出とクラス推定を同時に行うか否かの2種類のやり方が存在しています。

それぞれの特徴と、代表的な物体検知フレームワークがそのどちらに属しているかを以下の画像にて示します。

SSD

SSDは、Default Boxと呼ばれるバウンディングボックスを始めに用意しておき、検知する物体に合わせてDefault Boxを移動/変形する手法です。

Poolingによって解像度を落とした特徴マップの要素1つ1つに対して、各クラスへの分類のconfidenceおよび、DefaultBoxからの位置/サイズのオフセットを出力とします。

特徴マップのConvolution+Poolingを経るにつれて解像度が落ちていくのは、画像サイズは同じでピクセルサイズが大きくなっているイメージになります。解像度が落ちていくにつれて、大きな物体の検出が行われていきます。

Semantic segmentation

Semantic segmentationではPoolingで解像度を落としていった後に、解像度を上げてセグメンテーションを行う必要があります。

そもそも解像度を下げている理由は、受容野を広げるためです。狭い受容野では（猫の腕の一部を見ても犬の腕と見分けがつかないのと同じように）、物体の特徴を捉えることが難しくなるため受容野を広げる必要があったということです。

また、通常のConvolutionよりも解像度を落とさずに受容野を広げることが出来る畳み込みとしてWaveNetでも使われていたDilated convolutionを用いることが出来ます。

解像度を上げるために、Deconvolution/Transposed convolutionが行われます。

Poolingにより失われた輪郭情報については、畳み込みが進む前の出力を加えるelement-wise additionなどの手法によって補完します。

Seq2seq

系列（Sequence）を入力として、系列を出力するものであり、Encoder-Decoderモデルとも呼ばれています。

以下のような場面で使われています。

翻訳（日本語⇒英語）
音声認識（波形⇒テキスト）
チャットボット（テキスト⇒テキスト）

seq2seqの問題点として入力系列を１つのベクトルで表現しているために、入力系列が長くなると表現力が足りなくなり精度が落ちるという点があります。

Encoder

上の英語翻訳の例でEncoderを説明します。

日本語を入力としてバッチ内の系列の長さを固定長としてPaddingを加え、系列内の各時点の単語の次に続く単語の予測/生成を以下の様に行います。

しかし、実際にEncoderの結果で活用するのは予測結果ではなく、内部状態ベクトルです。

内部状態ベクトルは、Decoderへの入力として渡されます。

Decoder

Decoderは、Encoderからの入力として内部状態ベクトルを受け取る以外は、上で説明した「次の単語を予測する」普通のRNNです。

時刻tの入力単語 $\displaystyle{x_t}$ の予測結果 $\displaystyle{x_{t+1}}$ が時刻t+1の入力として用いられるため、予測が間違っていた場合に後ろの時刻の予測では入力自体が間違っていることになり、誤差が連鎖的に大きくなっていきます。この場合、学習が不安定になったり収束が遅くなったりするという問題が発生することがあります。

Teacher forcing

上記のSeq2seqの問題点を解消するための手法として、訓練時には常に正解の1時刻前の正しい入力を与えてあげるTeacher forcingという方法があります。

Teacher forcingによって学習されたモデルでは、Decoderの入力として与えられる系列は常に正しいものという前提で学習を進める振る舞いをするため、一度間違った単語が予測生成されてしまうとそこから単語の予測が狂いだす恐れがあります。

Scheduled sampling

Teacher forcingの問題を改善するための拡張手法です。

直前の時刻の予測で生成確立が最大となった単語を入力とする（シンプルなseq2seq）か、直前の時刻の正しい単語を入力とする（Teacher forcing）かを確率的にサンプリングして入力とします。学習初期はTeacher forcingの確率が高く、徐々に実際の翻訳テキスト生成時と近い状況としていきます。

BLEU

翻訳タスクの評価指標には、クロスエントロピーなどのタスク共通の指標に加えて翻訳専用のBLUEと呼ばれる指標が用いられます。

BLEUスコアは0~1の実数で表現され、値が高いほど良好な翻訳文であると判断されます。

式は以下の通りです。

$\displaystyle{ \verb|BLEU| = \verb|BP|_{\verb|BLEU|} \times e^{\left( \sum_{n=1}^N w_n \log p_n \right)} }$

$\displaystyle{ p_n = \frac{\sum_i \verb|翻訳文iと参照訳iで一致したn-gram数|}{\sum_i \verb|翻訳文i中の全n-gram数|} \\ w_n = 1/N }$

$\displaystyle{\verb|BP|_{\verb|BLEU|}}$ は、翻訳文が参照訳より短い場合に与えるペナルティ（brevity penalty）であり、翻訳文より参照訳が長い場合は1となります。

Nには通常4が用いられています。

※ 機械翻訳自動評価指標の比較より

Transformer

再帰や畳み込みを用いずにAttentionという機構を導入することで時系列データに対応することが出来ます。

以降では、各モジュールの内容について説明していきます。

Positional encoding

Transformerは系列の処理にRNNを用いないため、そのままだと単語列の語順を考慮することが出来ません。

よって、入力系列の埋め込み行列に対して、Positional encodingで作成した行列を加算することで単語の位置情報を埋め込みます。

Masking

特定のkeyに対してAttentionの重みを0にするために使われます。

Transformerでは以下の2種類のマスクが定義されています。

PADトークンに対するマスク
DecoderにてSelf attentionを行う際に各時刻において未来の情報に対するAttentionを行わせないためのマスク

Attention

RNN系のネットワークでは長い系列を取り扱うと、時系列的に離れるにつれて指数関数的に情報が失われていくという難点がありました。

一方、Attentionは重み付け和として、どこに注目すべきかを情報として与えることで離れた情報を無理なく扱えるようになりました。

Self attention

queryとkey, valueすべてに同じ情報を用いるAttentionです。

Transformerモデル図では、EncoderおよびDecoderの下部において、queryおよびkey, valueに同じ系列の隠れ状態を取ります。

あらゆる位置同士の単語の関係性を重みにとることができるため、局所的な位置しか参照できない畳み込みを用いた手法よりも良い性能を発揮できると言われています。

Source target attention

queryとkey, valueとで別の情報を用いるAttentionです。

Transformerモデル図では、Decoderブロック中央のMulti-head attentionにおいて、queryはDecoderの隠れ状態、key, valueはEncoderの隠れ状態を取ります。

Scaled dot-product attention

queryベクトルとkeyベクトルの関連度を内積によって求めSoftmax関数を通してAttention weightを得ます。

Attention weightとvalueベクトルの内積によってquery中の単語とkey中の単語との関連性の強さをvalueベクトルに反映させることが出来ます。

Multi-head attention

query, key, valueを小さな複数のheadに分割し、それぞれでAttentionを行った後、concatします。

モジュール内部では、Masking, Scaled dot-product attention, Multi-head attentionが組み合わされています。

Add & Norm

学習およびテストのエラーを低減させるために、出力に入力（residual）を加算し、その結果を正規化します。

Position-wise feedforward network

全結合層、ReLU、全結合層の順で変換をかけていき、位置情報を保持したまま順伝播させます。

$\displaystyle{ FFN(x) = max(0, \, x W_1 + b_1) W_2 + b_2 }$

最後に

後半は演習問題がなく解説のみの内容になってしまいましたが、RNNが言語処理や音声処理、CNNが物体検知に繋がっていく様子が見えて面白い内容となりました。

今回の記事はここまで。Kazuki Igetaでした😃

2021-06-06

E資格深層学習解説＆例題

E資格の受験資格を得るために必要な日本ディープラーニング協会認定講座であるラビットチャレンジの中で出題される演習問題をベースに、E資格の深層学習パートの例題と回答例をまとめました。

入力層～中間層
- Q1
  - 解答例
- Q2
  - 解答例
中間層で使われる活性化関数
出力層
勾配降下法（最急降下法）
誤差逆伝播法
- 誤差勾配の計算
- 誤差逆伝播法とは
  - Q9
    - 解答例
  - Q10
    - 解答例
勾配消失問題
- Q11
  - 解答例
- Q12
  - 解答例
勾配消失問題の解決法
- Q13
  - 解答例
- Q14
  - 解答例
学習率最適化手法
- Q15
  - 解答例
過学習
- 正則化のイメージ
  - Q16
    - 解答例
  - Q17
    - 解答例
  - Q18
    - 解答例
CNN (Convolutional Neural Network)
- Q19
  - 解答例
AlexNet
最後に

入力層～中間層

Q1

パーセプトロンの構造を表す以下の図式に、 $\displaystyle{x_1, x_2, x_3, x_4}$ として動物の種類を分類するのための入力データを書き入れてみてください。（無限通りの解答があります）

解答例

この解答例では、動物の分類に役立ちそうな特徴として、以下の画像の４つを選択しました。

Q2

パーセプトロンの入力、重み、バイアスから計算される総入力を求める計算をPythonで書いてみてください。

$\displaystyle{ W = \begin{pmatrix}1&3&4\\2&4&6\\4&5&6\end{pmatrix}, \, \boldsymbol{x} = \begin{pmatrix}2\\8\end{pmatrix}, \, \boldsymbol{b} = \begin{pmatrix}6\\3\\1\end{pmatrix} \nonumber \\ }$

$\displaystyle{ \begin{eqnarray} \begin{pmatrix}u_1\\u_2\\u_3\end{pmatrix} &=& \begin{pmatrix}w_{11} x_1 + w_{21} x_2 + b_1\\w_{12} x_1 + w_{22} x_2 + b_2\\w_{13} x_1 + w_{23} x_2 + b_3\end{pmatrix} \nonumber \\ &=& W \boldsymbol{x} + \boldsymbol{b} \nonumber \\ \end{eqnarray} }$

解答例

以下に解答例となるPythonスクリプトを示します。

$\displaystyle{W^{\mathrm{T}} \boldsymbol{x}}$ の部分では、 $\displaystyle{W^{\mathrm{T}}}$ によって2次元ベクトル $\displaystyle{\boldsymbol{x}}$ を3次元空間へ写像しています。

W = np.array([[1, 3, 5], [2, 4, 6]])
x = np.array([[2], [8]])
b = np.array([[6], [3], [1]]) 
u = W.T.dot(x) + b

中間層で使われる活性化関数

活性化関数（activation function）とは、入力の総和から次の層への出力の大きさを決める非線形の関数です。

ステップ関数

$\displaystyle{ f(x) = \begin{cases}1 \ \ (x \geq 0) \\ 0\left( x <0\right) \end{cases} }$

閾値を超えたら発火する関数であり、出力は常に1か0。
ステップ関数を用いた場合には線形分離可能なものしか学習できなかった。
現在ではほとんど使われていない。

シグモイド関数

$\displaystyle{ f(x) = \frac{1}{1 + e^{-x}} }$

0から1の間を緩やかに変化する関数。
シグモイド関数の微分は0から0.25の値を取るため、誤差逆伝播法において隠れ層（中間層）を遡るにつれて勾配が小さくなり勾配消失問題を引き起こす可能性がある。

ReLU関数

$\displaystyle{ f(x) = \begin{cases}x \ \ (x \gt 0) \\ 0 \ \ (x \leq 0) \end{cases} }$

現在最もよく使われている活性化関数。
勾配消失問題の回避とスパース化に貢献することで良い成果をもたらしている。
- ReLUの派生として、Leaky ReLUやParametric ReLU, Randomized ReLUなどがあるが、どれが一番良いかを一概に決めることは出来ない。

Q3

線形と非線形の違いを図に書いて簡易的に説明してみてください。

解答例

線形な関数は、

加法性: $\displaystyle{f(x+y) = f(x) + f(y)}$
斉次性: $\displaystyle{f(kx) = kf(x)}$

非線形な関数は、加法性および斉次性を満たさない。

Q4

ReLU関数をPythonにて実装してみてください。

解答例

import numpy as np


def relu(x)
    return np.maximum(0, x)

出力層

損失関数（loss function）

損失関数とは、予測と訓練データの正解の誤差を定量的に測定する為の関数です。

学習フェーズにおいて、最適なパラメータに近づけるための指標として使われています。

損失関数には様々な種類が存在しており、これを使わなければいけないというような決まりはありません。回帰や分類といったタスクの種類や、データの性質などによって利用されている損失関数が異なる場合があります。

平均二乗誤差（MSE）

予測値と訓練データの正解ラベルとの残差平方和。

$\displaystyle{ MSE = \frac{1}{2} \sum_{i=1}^n (\hat{y_i} - y_i)^2 }$

Q5

MSEでは、なぜ予測値と正解ラベルの差をそのまま使わずに2乗しているか答えてみてください。加えて、残差平方和を $\displaystyle{1/2}$ する理由も答えてみてください。

解答例

2乗する理由
- 2乗しない場合には各ラベルの誤差に正負両方の値が発生し、全体の誤差を上手く表すことが出来ない。解決方法として、残差の絶対値を取る平均絶対誤差（MAE）やMSEなどが存在する。
$\displaystyle{1/2}$ する理由
- ネットワークの学習時に行う誤差逆伝播の計算に置いて損失関数の微分が用いられる。2次式の微分で発生する係数を打ち消し計算式を簡単にする。

出力層で使われる活性化関数

活性化関数については、中間層で使われる活性化関数で説明しましたが、実は中間層と出力層では使われる活性化関数が異なっています。

出力層と中間層の違い

値の強弱
- 中間層の活性化関数は、ベクトルの要素間の比率を非線形変換によって変化する。
- 出力層の活性化関数は、ベクトルの要素間の比率を一定に保ったまま変換する。
確率出力
- 分類問題における出力層の活性化関数は、出力となるベクトルの要素を確立として表すためにその総和を1とする。

	回帰	二値分類	多クラス分類
出力層で使われる代表的な活性化関数	恒等写像 $\displaystyle{f(u) = u}$	シグモイド関数 $\displaystyle{f(u) = \frac{1}{1 + e^{-u}}}$	ソフトマックス関数 $\displaystyle{f(i, \boldsymbol{u}) = \frac{e^{u_i}}{\sum_{k=1}^K e^{u_k}}}$
代表的な損失関数	平均二乗誤差（MSE）	交差エントロピー誤差（cross entropy loss）	交差エントロピー誤差（cross entropy loss）

Q6

$\displaystyle{f(i, \boldsymbol{u}) = \frac{e^{u_i}}{\sum_{k=1}^K e^{u_k}}}$ は、総入力のベクトル $\displaystyle{\boldsymbol{u}}$ およびクラスラベル $\displaystyle{i}$ を引数として、データがクラス $\displaystyle{i}$ に属する確率をスカラで返す関数になっています。

一方、実際の場面で使われるのは以下の式(1)の様に、総入力のベクトル $\displaystyle{\boldsymbol{u}}$ を引数として、データが各クラスに属する確率をベクトルで返す関数です。

$\displaystyle{ f(\boldsymbol{u}) = \begin{pmatrix}\frac{e^{u_1}}{\sum_{k=1}^K e^{u_k}}\\\frac{e^{u_2}}{\sum_{i=1}^K e^{u_k}}\\\vdots\\\frac{e^{u_K}}{\sum_{k=1}^K e^{u_k}}\end{pmatrix} \ \ \ where \ \ \boldsymbol{u} = (u_1 \, u_2 \, \ldots \, u_K )^{\mathrm{T}} \ \ \ \cdots (1) }$

上記式(1)をPythonで実装してみてください。

解答例

2行目のu = u - np.max(u)は3行目の計算時に発生し得るオーバーフローの回避を目的とした実装です。

def softmax(u):
    u = u - np.max(u)
    return np.exp(u) / np.sum(np.exp(u))

オーバーフロー回避について説明するにあたって、まずnumpyで扱う浮動小数について説明していきます。

浮動小数について

numpyの浮動小数を表すnumpy.float64型は $\displaystyle{-1.7976931348623157 \times 10^{308} \le f \le 1.7976931348623157 \times 10^{308}}$ の範囲を表すことが出来ます。

以下のWikipediaページにてDouble-precision examplesから、数値例を見てみると浮動小数の値の表し方が理解しやすいです。

en.wikipedia.org

Softmax関数はネイピア数の指数が使われていますが、例えば、Softmax関数の引数の入力ベクトル要素の1つに1000があったとすると関数内部で $\displaystyle{e^{1000}}$ が作られ、numpy.float64の最大値を超えて正しく計算ができない桁あふれ（オーバーフロー）が発生してしまいます。

入力値が1000を超えるというのはよくあることなので、このままではオーバーフローが原因でSoftmax関数を使える場面がかなり限定的になってしまうことになります。

以上を踏まえて、オーバーフロー回避方法について以下に説明します。

オーバーフロー回避

以下の式の通り、分子と分母のネイピア数の指数の値に同じ値を加算しても式自体の値には変化がありません。

そこで、ネイピア数の指数 $\displaystyle{u_i}$ から $\displaystyle{\max(\boldsymbol{u})}$ を引く処理をしてあげることで、Softmax関数の戻り値を変えずにオーバフローを回避することが出来ることになります。

$\displaystyle{ \begin{eqnarray} y_i &=& \frac{e^{u_i}}{\sum_{k=1}^K e^{u_k}} \nonumber \\ &=& \frac{C e^{u_i}}{C \sum_{k=1}^K e^{u_k}} \nonumber \\ &=& \frac{e^{u_i + \log{C}}}{\sum_{k=1}^K e^{u_k + \log{C}}} \ \ \ where \ \ C = e^{\log C} \nonumber \\ &=& \frac{e^{u_i + C'}}{\sum_{k=1}^K e^{u_k + C'}} \nonumber \\ &=& \frac{e^{u_i - \max(\boldsymbol{u})}}{\sum_{k=1}^K e^{u_k - \max(\boldsymbol{u})}} \nonumber \\ \end{eqnarray} }$

勾配降下法（最急降下法）

バッチ勾配降下法とも呼ばれます。

損失関数 $\displaystyle{E(\boldsymbol{w})}$ が最小となる $\displaystyle{\boldsymbol{w}}$ を数値的に求める手法の1つであり、以下の式で定義されます。

学習1エポックで更新される $\displaystyle{\boldsymbol{w}}$ の大きさは学習率 $\displaystyle{\varepsilon}$ によって指定されます。

$\displaystyle{\boldsymbol{w}_{t+1} = \boldsymbol{w}_t - \eta \nabla E(\boldsymbol{w}) }$

Q7

$\displaystyle{\boldsymbol{u} = X \boldsymbol{w}}$ において損失関数MSEが最小となる $\displaystyle{\boldsymbol{w}}$ を勾配降下法で求める関数をPythonで実装してみてください。

なお、引数として、入力データとなる $\displaystyle{n \times d}$ 行列 $\displaystyle{X}$ 、イテレーション回数上限、学習率 $\displaystyle{\eta}$ を取るように実装してみてください。

解答例

問題の条件では、式変形によって $\displaystyle{ \boldsymbol{w} = (X^\mathrm{T} X)^{-1} X^\mathrm{T} \boldsymbol{y} \ }$ を得ることが出来るため、以下の関数が解答例例となります。

この式変形が出来る理由が分からない場合は、基礎的な機械学習アルゴリズムの原理に説明があるので読んでみてください。

def gradient_decent(X_train, max_iter, eta):
    w = np.zeros(X_train.shape[1]).reshape(-1,1)
    for _ in range(max_iter):
        w_prev = np.copy(w)
        u_hat = sigmoid(np.dot(X_train, w))
        grad = np.dot(X_train.T, (u_hat - u_train))
        w -= eta * grad
        if np.allclose(w, w_prev):
            return w
    return w

確率的勾配降下法（SGD）

ランダムに抽出したサンプルの誤差を最小化する手法です。

勾配降下法と比較したSGDメリットは以下の通りです。 - データが冗長な場合の計算コスト軽減 - 望まない局所極小解に収束するリスク軽減 - オンライン学習が可能 - 学習開始後に継続してデータを集めて学習に利用できる - 勾配降下法はオンライン学習に対してバッチ学習と呼ばれる

Q8

オンライン学習について説明してみてください。

解答例

学習データが入ってくるたびにパラメータを更新し、学習を進めていく方法のことです。画像を訓練データとする深層学習では特にデータサイズが大きくなるため、1度に全データをメモリに展開する必要のあるバッチ学習ではメモリ容量不足が発生しやすく、オンライン学習の利用が良く用いられています。

ミニバッチ勾配降下法

オンライン学習の要素をバッチ勾配降下法に取り込んだ方法です。ランダムに分割したデータの集合（ミニバッチ）に属するサンプルの平均誤差を最小化します。

深層学習においては、最も一般的な勾配降下法です。

ミニバッチ勾配降下法のメリットは以下の通りです。

並列処理により処理時間を短縮できる
メモリ消費量を押さえられる

誤差逆伝播法

誤差勾配の計算

勾配 $\displaystyle{\nabla E = \frac{\partial E}{\partial \boldsymbol{w}}}$ を求める方法として、以下の様に微小範囲における変化量を求める数値微分という方法があります。

$\displaystyle{ \frac{\partial E}{\partial w_m} \simeq \frac{E(w_m + h) - E(w_m - h)}{2 h} }$

この方法では、各層のパラメータ $\displaystyle{w}$ の数だけ同じ計算を繰り返し行う必要があり計算負荷が高いため、実際には誤差逆伝播法が用いられています。

誤差逆伝播法とは

計算結果（誤差）から微分を逆算することで不要な再帰的計算を避けて各パラメータの微分を算出することが出来る方法です。

Q9

以下のソースコードでは、SGDによって誤差を最小化する際に誤差逆伝播法を用いており、出力層の微分delta2の値を1つ前の層の微分delta1の計算に再利用しています。

出力層の微分delta2を再利用しているコードを抜きだして答えてみてください。

解答例

delta1 = np.dot(delta2, W2.T) * functions.d_sigmoid(z1)

Q10

微分に対応するPythonコードをQ9で示したソースコードから抜き出して、以下の表の空白を埋めてみてください。

なお、ソースコードで実装されているニューラルネットワークは以下の画像の構成になっています。

微分	Pythonコード
$\displaystyle{ \frac{\partial E}{\partial \boldsymbol{y}} }$
$\displaystyle{ \frac{\partial E}{\partial \boldsymbol{y}} \frac{\partial \boldsymbol{y}}{\partial \boldsymbol{u}^{(2)}} \frac{\partial \boldsymbol{u}^{(2)}}{\partial \boldsymbol{w}^{(2)}} }$
$\displaystyle{ \frac{\partial E}{\partial \boldsymbol{y}} \frac{\partial \boldsymbol{y}}{\partial \boldsymbol{u}^{(2)}} \frac{\partial \boldsymbol{u}^{(2)}}{\partial \boldsymbol{z}} \frac{\partial \boldsymbol{z}}{\partial \boldsymbol{u}^{(1)}} }$

解答例

微分	Pythonコード
$\displaystyle{ \frac{\partial E}{\partial \boldsymbol{y}} }$	`delta2 = d_mean_squared_error(d, y)`
$\displaystyle{ \frac{\partial E}{\partial \boldsymbol{y}} \frac{\partial \boldsymbol{y}}{\partial \boldsymbol{u}^{(2)}} \frac{\partial \boldsymbol{u}^{(2)}}{\partial \boldsymbol{w}^{(2)}} }$	`grad['W2'] = np.dot(z1.T, delta2)`
$\displaystyle{ \frac{\partial E}{\partial \boldsymbol{y}} \frac{\partial \boldsymbol{y}}{\partial \boldsymbol{u}^{(2)}} \frac{\partial \boldsymbol{u}^{(2)}}{\partial \boldsymbol{z}} \frac{\partial \boldsymbol{z}}{\partial \boldsymbol{u}^{(1)}} }$	`delta1 = np.dot(delta2, W2.T) * d_sigmoid(z1)`

勾配消失問題

誤差を逆伝播しながら誤差を各パラメータで微分した値を求めていくにあたり、逆伝播で層を遡るにつれて勾配の値がどんどんと小さくなっていきやがて消えてしまうという問題は勾配消失問題と呼ばれています。

Q11

連鎖率の原理を使って、以下の式の $\displaystyle{\frac{dz}{dx}}$ を求めてみてください。

$\displaystyle{ z = t^2 \\ t = x + y }$

解答例

この計算は、誤差逆伝播法の中で沢山でてくる計算でしたね。回答は以下の通りです。

$\displaystyle{ \frac{dz}{dt} = 2t \\ \frac{dt}{dx} = 1 \\ \frac{dz}{dx} = \frac{dz}{dt} \frac{dt}{dx} = 2t \cdot 1 = 2t = 2(x + y) }$

Q12

シグモイド関数の導関数は、入力が0のときに最大値を取ります。その最大値を答えてみてください。

解答例

答えは、0.25です。

解説

シグモイド関数 $\displaystyle{f(x) = \frac{1}{1 + e^{-x}}}$ の導関数は、 $\displaystyle{f'(x) = (1 - f(x)) \cdot f(x)}$ となります。

$\displaystyle{f(x)}$ を $\displaystyle{t}$ とおき、tで微分したものを0とおくと、 $\displaystyle{f(x) = 0.5}$ のときに $\displaystyle{f'(x)}$ が最大になることが分かります。

$\displaystyle{ \frac{d}{dt} (1-t) \cdot t = 1 -2t = 0 \\ \therefore t = f(x) = 0.5 }$

以下の通り、 $\displaystyle{f(0) = 0.5}$ となるため、シグモイド関数の導関数 $\displaystyle{f'(x)}$ は $\displaystyle{x = 0}$ のとき最大値0.25を取ることが分かりました。

$\displaystyle{ f(0) = \frac{1}{1 + e^{-0}} = 0.5 \\ \therefore f'(0) = (1 - f(0)) \cdot f(0) = (1 - 0.5) \cdot 0.5 = 0.25 }$

活性化関数にシグモイド関数を選択すると中間層１つを誤差逆伝播する度に勾配が最大でも0.25倍になってしまうため、中間層が増えると容易に勾配消失が発生してしまうことが分かりますね。

勾配消失問題の解決法

活性化関数の選択
- 例えばReLU関数を選択した場合、勾配が0または1となるため、活性化関数による勾配消失問題を防ぐことが出来る。また予測に役に立たないパラメータは勾配を0とすることでスパース化に役立つ。
重みの初期値設定
- 活性化関数に合わせた重みの初期値設定が存在する。
- シグモイド関数およびReLU関数には、Xavierの初期値を用いることで、勾配消失を防ぎつつ活性化関数を通した後の値の分布が広がる（表現力の抑制を防げる）。
バッチ正規化
- 学習速度向上および過学習抑制などが期待できる。

Q13

重みの初期値を0に設定すると、どのような問題が発生するか答えてみてください。

解答例

重みの初期値を0に設定すると、誤差逆伝播において全ての重みの値が均一に更新されるため、多数の重みパラメータを持つ意味がなくなってしまいます。

Q14

深層学習では一般に必要とするデータ数が多く、メモリなどの都合ですべてをまとめてバッチで計算することができません。

以下のコードは、データを少数のまとまりに分けて計算を行うミニバッチ学習を実装しています。■および▲に当てはまる内容を答えてみてください。

def train(data_x, data_t, n_epoch, batch_size):
    '''
    data_x: training data (features)
    data_t: training data (labels)
    n_epoch: number of epochs
    batch_size: mini batch size
    '''
    n = len(data_x)
    for epoch in range(n_epoch)
        shuffle_idx = np.random. permutation(N)
        for i in range(0, n, batch_size):
            i_end = i + batch_size
            batch_x, batch_t = data_x[■], data_t[▲]
            _update(batch_x, batch_t)

解答例

バッチサイズの分だけデータを取り出す処理が回答として入ります。

def train(data_x, data_t, n_epoch, batch_size):
    '''
    data_x: training data (features)
    data_t: training data (labels)
    n_epoch: number of epochs
    batch_size: mini batch size
    '''
    n = len(data_x)
    for epoch in range(n_epoch)
        shuffle_idx = np.random. permutation(N)
        for i in range(0, n, batch_size):
            i_end = i + batch_size
            batch_x, batch_t = data_x[i:i_end], data_t[i:i_end]
            _update(batch_x, batch_t)

学習率最適化手法

学習率が大きい場合には、重みが最適値にいつまでもたどり着かずに発散してしまう可能性があります。

一方、学習率の値が小さい場合には、発散することはなくとも収束するまでに長い時間を要します。また、大局的最適値ではなく局所的最適値に収束しやすくなります。

そこで、重みの更新量を状況によって変化させる各種の学習率最適化手法が考案されてきました。

Q15

モーメンタム・AdaGrad・RMSPropの特徴について、それぞれ簡潔に説明してみてください。

解答例

現在定番の手法として用いられているAdamは、以下の通り、モーメンタムとRMSPropを組み合わせたものです。

手法	特徴
モーメンタム	今までの動き（慣性）を考慮することで、勾配降下法の振動を移動平均と同じ理屈で抑える手法
AdaGrad	今までの更新量が大きくなるにつれて、現在の更新量を小さくすることで勾配降下法の振動を抑制するという考え方をパラメータごとに適用した手法
RMSProp	AdaGradに対して、過去の勾配の影響がどんどん減っていく機能を追加した手法
Adam	移動平均で振動を抑制するモーメンタムと学習率を調整して振動を抑制するRMSPropを組み合わせた手法

過学習

過学習の原因の1つとして、一部の特徴量を過大評価してしまっている場合、つまり重みが大きくなりすぎてしまっている場合があります。

その対策として、損失関数に正則化項を加えることで重みが大きくなりすぎないように抑えて過学習を抑制する正則化という方法があります。

しかし、ニューラルネットワークのモデルが複雑になってくると正則化だけでは過学習の対応が困難になってきます。そこでニューロンをランダムに消去しながら学習することで過学習を抑制するドロップアウトという手法が良く用いられています。

正則化のイメージ

L1正則化で行われていることを3Dでイメージしてみると、以下の図のようになります。

正則化項の持つ角が、最小化する式にうっすらと反映されているのが見えます。この角で最小化されることが多いため、重要でない重みの値が0とみなされスパース化が行われます。

次に、L2正則化で行われていることを3Dでイメージしてみると、以下の図のようになります。

L1正則化と同様に、正則化項を加算することによって最小化する式は誤差関数から変形して最小値も変わっていますが、最小値を取った際に重みが0となりやすいような形にはなっていないことが分かります。

Q16

以下の図は上記3Dイメージの等高線を描画したものです。L1正則化を表しているグラフはどちらであるか答えてみてください。

解答例

右のグラフがL1正則化を表しています。

L1ノルムを用いるラッソ正則化がL1正則化と呼ばれています。

Q17

以下のPythonコードは、L2正則化を適用した場合にパラメータの更新を行うプログラムです。

あるパラメータparamと正則化がないときにそのパラメータに伝播される誤差の勾配gradが与えられたとします。

最終的な勾配を計算する■に当てはまるコードを以下の4つから選んでみてください。

(1) np.sum(param**2)

(2) np.sum(param)

(3) param**2

(4) param

def ridge(param, grad, rate):
    '''
    param: target parameter
    grad: gradients to param
    rate: lasso coefficient
    '''
    grad += rate * ■

解答例

答えは、(4)です。

リッジ正則化を行うために損失関数に正則化項を加えた式は以下の様になります。

$\displaystyle{ \begin{eqnarray} E(\boldsymbol{w}) + \frac{1}{p} \lambda \|\boldsymbol{w}\|_p &=& E(\boldsymbol{w}) + \frac{1}{2} \lambda \|\boldsymbol{w}\|_2^2 \ \ \ where \ \ p = 2 \nonumber \\ &=& E(\boldsymbol{w}) + \frac{1}{2} \lambda \boldsymbol{w}^{\mathrm{T}} \boldsymbol{w} \nonumber \\ \end{eqnarray} }$

上記の式に置いて、第1項の微分がPythonコードでいうgradに当たり、第2項の微分が今回の解答となります。

というわけで、第2項を微分してみると、 $\displaystyle{\frac{d}{d \boldsymbol{w}} \frac{1}{2} \lambda \boldsymbol{w}^{\mathrm{T}} \boldsymbol{w} = \lambda \boldsymbol{w} }$ となるため、穴埋めで■にあたる部分は $\displaystyle{\boldsymbol{w}}$ つまりparamが解答となります。

def ridge(param, grad, rate):
    '''
    param: target parameter
    grad: gradients to param
    rate: lasso coefficient
    '''
    grad += rate * param

Q18

以下のPythonコードは、L1正則化を適用した場合にパラメータの更新を行うプログラムです。

あるパラメータparamと正則化がないときにそのパラメータに伝播される誤差の勾配gradが与えられたとします。

最終的な勾配を計算する■に当てはまるコードを以下の4つから選んでみてください。

(1) np.maximum(param, 0)

(2) np.minimum(param, 0)

(3) np.sign(param)

(4) np.abs(param)

def ridge(param, grad, rate):
    '''
    param: target parameter
    grad: gradients to param
    rate: lasso coefficient
    '''
    x = rate * ■
    grad += rate * x

解答例

答えは(3)です。

ラッソ正則化を行うために損失関数に正則化項を加えた式は以下の様になります。

$\displaystyle{ \begin{eqnarray} E(\boldsymbol{w}) + \frac{1}{p} \lambda \|\boldsymbol{w}\|_p &=& E(\boldsymbol{w}) + \lambda \|\boldsymbol{w}\|_1 \ \ \ where \ \ p = 1 \nonumber \\ \end{eqnarray} }$

つまり、Q17で行ったのと同じように第2項 $\displaystyle{\lambda |\boldsymbol{w}|_1}$ を $\displaystyle{\boldsymbol{w}}$ で微分したいわけです。皆さんやり方は分かりますか？

L1ノルムの微分なので、以下のグラフような絶対値のついた関数の微分を考える必要があります。

このグラフより、絶対値の影響で $\displaystyle{w > 0}$ の座標から横軸を基準にグラフが折り返されていることが分かります。

この関数はなめらかでないため微分不可能です。微分を行うためには、右微分 $\displaystyle{d^+(|w|)}$ と左微分 $\displaystyle{d^-(|w|)}$ を行う必要があります。

$\displaystyle{ d^+(|w|) = \lim_{h \to +0} \frac{|w + h| - |w|}{h} = \lim_{h \to +0} \frac{(w + h) - (w)}{h} = 1 }$

$\displaystyle{ d^-(|w|) = \lim_{h \to +0} \frac{|w + h| - |w|}{h} = \lim_{h \to +0} \frac{-(w + h) - (-w)}{h} = -1 }$

以上より、 $\displaystyle{w}$ の符号によって、 $\displaystyle{|w|}$ の微分は+1または-1になることが分かりました。

つまり、第2項の $\displaystyle{\boldsymbol{w}}$ での偏微分は以下の式で表すことが出来ます。

$\displaystyle{ \frac{d}{d \boldsymbol{w}} \lambda \|\boldsymbol{w}\|_1 = \begin{cases}\lambda \ \ \ (w_i > 0) \\0 \ \ \ (w_i = 0) \\ -\lambda \ \ \ (w_i < 0) \end{cases} }$

したがって、穴埋めで■にあたる部分はベクトル要素の符号に応じて1, 0, -1を返すnp.sign(param)が解答となります。

def ridge(param, grad, rate):
    '''
    param: target parameter
    grad: gradients to param
    rate: lasso coefficient
    '''
    x = rate * np.sign(param)
    grad += rate * x

CNN (Convolutional Neural Network)

画像データや音声データなどの入力データの形に意味があるデータの学習によく使われる手法です。

畳み込み層とプーリング層（サブサンプリング層）によって形状に意味を持たせた特徴量を行列として作成し、Flatten, Global Max Pooling, Global Average Poolingなどによって1次元ベクトルに変換した後は全結合層と呼ばれる形状を意識しない通常のDNNの処理が行われていきます。

Q19

サイズ6×6の入力画像を、サイズ2×2のフィルタで畳み込んだ時の出力画像のサイズを答えてみてください。

このときストライドとパディングを1とします。

解答例

以下の公式で畳み込み後の出力サイズを計算することが出来ます。

$\displaystyle{ 出力画像の高さ = \frac{画像の高さ + 2 \times パディング高さ - フィルタ高さ}{ストライド} + 1 \\ 出力画像の幅 = \frac{画像の幅 + 2 \times パディング幅 - フィルタ幅}{ストライド} + 1 \\ }$

よって、答えは以下の通り、7×7となります。

$\displaystyle{ 出力画像の高さ = \frac{6 + 2 \times 1 - 2}{1} + 1 = 7\\ 出力画像の幅 = \frac{6 + 2 \times 1 - 2}{1} + 1 = 7\\ }$

AlexNet

画像内の物体認識の精度を競う国際大会ILSVRCにおいて2012年に優勝を果たした際に使われたAlexNetのアーキテクチャをCNNの代表例として以下に示します。

上記アーキテクチャの中では以下の内容が含まれています。

3つの畳み込み層
2つのMaxプーリング層
3つの全結合層
- ドロップアウト

最後に

浮動小数についてに記載した符号・指数部・仮数部といったbitレベルで、numpy.float64型自体の理解をE資格で問われることはないだろうとは思います。

だた、機械学習アルゴリズムの実装を自分で行う場合にはメモリを意識したプログラミングができると意図しないエラーで困ることが減るんじゃないかと思いました。

今回の記事はここまで。Kazuki Igetaでした😃

2021-05-28

基礎的な機械学習アルゴリズムの原理

機械学習応用数学

今回は機械学習について基礎的な重要項目のまとめを行ったので紹介していきます😃

本記事の解説は、各種モデルの数学的な理解を目的としています。

E資格の認定プログラムであるラビットチャレンジの講義や、書籍である機械学習のエッセンスを参考に記載しています。目次の中で★のついた項目は、私の中で特に重要な学びを得られた部分なので重点的に説明を行います。

機械学習の理論を理解するにあたって応用数学に不安のある方は、この記事より先に以下の記事を読んでもらえると機械学習で必要となる基礎部分をある程度抑えることが出来るかと思います。

kazukiigeta.com

★線形回帰モデル
非線形回帰モデル
- 実装
ロジスティック回帰モデル
- 勾配降下法
- 実装
主成分分析（PCA）
- 実装
k近傍法（kNN）
- 実装
k-means
- 実装
SVM
- 実装
未学習/過学習
参考文献
最後に

★線形回帰モデル

定義

線形とは、簡単に言うと比例のことです。回帰は、連続値の予測を行うことです。

線形回帰モデルを、方程式表記・行列表記の両記法で理解できるようにする必要があります。特に行列表記は、私を含む多くの人にとって今まで最も目に触れる機会の少ない表記法であると思います。

方程式表記と行列表記を頭の中で行き来できるようにしておくと、今後の学習で計算の理解に非常に役に立ちそうです。

方程式表記

yがターゲット変数、xが説明変数、wが回帰係数になっています。

$\displaystyle{ y_{1} = w_{0} + w_{1 1}x_{1 1} + w_{1 2}x_{1 2} + \cdots + w_{1 m}x_{1 m} + \varepsilon_1 \tag{1} \\ y_{2} = w_{0} + w_{2 1}x_{2 1} + w_{2 2}x_{2 2} + \cdots + w_{2 m}x_{2 m} + \varepsilon_2 \\ \vdots \\ y_{n} = w_{0} + w_{n 1}x_{n 1} + w_{n 2}x_{n 2} + \cdots + w_{n m}x_{n m} + \varepsilon_n \\ }$

1つ目の式のみに注目すると以下の様にベクトルで表すことが出来ます。

$\displaystyle{ y_1 = \boldsymbol{w} ^ \mathrm{T} \boldsymbol{x_1} + \varepsilon_1 \tag{2} \\ \mathrm{where} \ \ \boldsymbol{w} = (w_{0} \, w_1 \, w_2 \, \ldots \, w_m) ^ \mathrm{T}, \boldsymbol{x_1} = (1 \, x_{1 1} \, x_{1 2} \, \ldots \, x_{1 m}) }$

方程式の全体に対しては、以下の様に行列で表現することができます。

行列表記

$\displaystyle{ \boldsymbol{y} = \boldsymbol{X} \boldsymbol{w} + \boldsymbol{\varepsilon} \tag{3} \\ }$

$\displaystyle{ \left( \begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \end{array} \right) = \begin{pmatrix}1&x_{1 1}&x_{1 2}&\cdots&x_{1 m}\\1&x_{1 2}&x_{2 2}&\cdots&x_{2 m}\\\vdots&\vdots&\vdots&\ddots&\vdots\\1&x_{n 1}&x_{n 2}&\cdots&x_{n m}\end{pmatrix} \begin{pmatrix}w_0\\w_1\\\vdots\\w_m\end{pmatrix} + \begin{pmatrix}\varepsilon_1\\\varepsilon_2\\\vdots\\\varepsilon_n\end{pmatrix} \tag{4} }$

学習

学習フェーズにおいては、 $\displaystyle{\boldsymbol{y}}$ や $\displaystyle{\boldsymbol{x}}$ といったパラメータは、学習データから得られる既知のものであり、一方、パラメータ $\displaystyle{\boldsymbol{w}}$ は未知のものです。学習を行うというのは、最適な未知のパラメータ $\displaystyle{\boldsymbol{w}}$ を求めることに他なりません。

最適なwを求めるための最も一般的なのは、損失関数として平均二乗誤差 (Mean Squared Error; MSE)を用い、MSEが最小になる $\displaystyle{\boldsymbol{w}}$ を選択するという方法です。線形モデルの場合は、MSEは下に凸の2次式であるため、MSEが最小となる $\displaystyle{\boldsymbol{w}}$ を解析的に求めることができます。

MSEを $\displaystyle{\boldsymbol{w}}$ で偏微分したものが0となる $\displaystyle{\boldsymbol{w}}$ を求めることは、MSEが最小となる $\displaystyle{\boldsymbol{w}}$ を求めることと同義です。

$\displaystyle{ \hat{w} = arg \ min_{\boldsymbol{w} \in \mathbb{R}} MSE_{train} \tag{5} \\ }$

$\displaystyle{ \frac{\partial MSE_{train}} {\partial{\boldsymbol{w}}} = 0 \tag{6} }$

機械学習の様に変数が多数存在する場面では、式(6)を行列を用いて解くのが効率が良いです。行列を使って式(6)を解く方法を丁寧な式展開で以下に示します。解くというのは、ここでは回帰係数行列 $\displaystyle{\boldsymbol{w}}$ を求めることを意味しています。

以上より、回帰係数行列 $\displaystyle{\boldsymbol{w}}$ を以下の式(7)で求めることが出来ます。

$\displaystyle{ \boldsymbol{w} = (X^\mathrm{T} X)^{-1} X^\mathrm{T} \boldsymbol{y} \tag{7} \\ }$

今回は損失関数にMSEを使いました。しかし、必ずしもMSEを使わなければいけないわけではいけません。

損失関数の選択

今回の様に損失関数にMSEを用いた場合には、2乗している分、外れ値の影響を強く受けることになります。外れ値を取り除くことができない場合には、Robustな損失関数としてHuber損失などを使うこともできます。 Huber損失とは、損失が大きいとMAEの様に1次形式をとり、損失が小さいとMSEと同様の2次形式をとる損失関数です。

予測

式(3), (7)より、以下の式(8)にて予測値を得ることが出来るようになります。

$\displaystyle{ \boldsymbol{\hat{y}} = X (X^\mathrm{T} X)^{-1} X^\mathrm{T} \boldsymbol{y} \tag{8} \\ }$

実装

損失関数にMSEを用いて単回帰分析と重回帰分析を実装しました。重回帰分析には、上で説明してきた行列の計算を用いて学習および予測を行っています。

非線形回帰モデル

以下のグラフを直線で近似するのが無理があるように、非線形な構造を内在する現象に対して直線/超平面でデータ構造を捉えることは出来ません。

そこで、線形回帰モデルを非線形性に対応させる方法である基底展開法を説明していきます。基底展開法とは、基底関数と呼ばれる既知の非線形関数によって説明変数を非線形変換した値とパラメータベクトル $\displaystyle{\boldsymbol{w}}$ の線形結合を回帰関数として用いる方法です。

このように、非線形モデルによって回帰タスクを解くことを、非線形回帰と呼びます。

実際に存在する線形回帰モデルとの違いは、線形回帰でいう行列Xを非線形変換した行列Φ(x)に置き換えてあげるだけです。以下の実装によって実例を見ていきます。

実装

$\displaystyle{\sin}$ 関数で作成された値を、3次関数を既定関数とした非線形モデルにて学習/予測するモデルを実装しました。上述した行列計算を用いない方法での線形回帰モデルの式の導出についても、この中で説明しています。

ロジスティック回帰モデル

ロジスティック回帰は、上で説明してきた線形回帰を回帰ではなく分類に用いる機械学習モデルです。以下にその構造を示します。

$\displaystyle{ \boldsymbol{w} = (w_1 \, w_2 \, \cdots \, w_m)^\mathrm{T} \in \mathbb{R}^m }$

$\displaystyle{ \hat{y} = \boldsymbol{w}^\mathrm{T} \boldsymbol{x} + w_0 = \sum_{j=1}^m {w_j x_j} + w_0 }$

$\displaystyle{ 0 \leq y \leq 1 }$

上の図の通り、線形回帰モデルの出力である連続値をシグモイド関数を通して $\displaystyle{y=1}$ になる確率を得ることが出来ます。

線形回帰モデルにおいて損失関数にMSEを用いた場合には $\displaystyle{\frac{\partial {MSE}}{\partial \boldsymbol{w}}}$ が0になる $\displaystyle{\boldsymbol{w}}$ を解析的に求めることが出来ましたが、ロジスティック回帰モデルにおいて損失関数に対数尤度関数を用いた場合には対数尤度関数の $\displaystyle{\boldsymbol{w}}$ に関する偏微分が0となる値を解析的に求めることは困難です。

解析的に求めることが難しい場合には、勾配降下法（Gradient descent）を用いて数値的に解を求めるのが機械学習の基本的な考え方です。

勾配降下法

数値的に解を求める代表的な方法として勾配降下法（最急降下法）があります。勾配降下法の仕組みは2変数関数を3次元空間で表現してみるとイメージしやすいと思います。

上の3次元表示のグラフは、 $\displaystyle{x}$ と $\displaystyle{y}$ の変化に応じて $\displaystyle{f(x,y)}$ 軸方向の値が変化することで3次元の形状が表現されています。

$\displaystyle{f(x,y)=const.}$ となるとき、いくつかのパターンを同時に $\displaystyle{x, y}$ 平面に描画すると、 $\displaystyle{f(x,y)}$ 等高線を得ることが出来ます。山が2つ存在するような2変数関数の等高線を同時に描画したイメージを以下に示します。

上記の図は、勾配降下法により以下の流れで局所最適解を求めている様子を表しています。

初期値として最初の点（今回は図の下の方）を選ぶ
点と $\displaystyle{f(x,y)}$ が等しい等高線に対する接線の法線ベクトル $\displaystyle{\nabla f}$ を求める（ $\displaystyle{\nabla f}$ は勾配が最も大きい方向を指す）
法線ベクトルと3次元図形の交点のうち、関数値 $\displaystyle{f(x,y)}$ が最大or最小となる点を求める（直線探索と呼ばれる）
更新される長さが一定値以下になるまで2から3までを繰り返す

実装

ロジスティック回帰による二値分類を実装しました。この中では、行列計算を使ってロジスティック回帰の学習/予測を行うための式の導出についても説明しています。

主成分分析（PCA）

主成分分析（PCA）とは、教師無し学習の1種です。多変量データを低次元空間に射影することで次元圧縮することが出来ます。圧縮時には、情報の損失をなるべく小さくするために射影後の点の散らばりが出来るだけ大きくなるように考慮されます。つまり、次元圧縮後の分散を最大化するという最適化問題になっています。

以下の実装にて、式の導出と共に説明を行います。

実装

k近傍法（kNN）

k近傍法は、距離指標に基づいて訓練データの中から分類したいデータ点に最も近いk個のサンプルを抽出し、その中の多数決によってクラスラベルを決定するというアルゴリズムで、教師無し学習の１つです。

訓練データから、入力とクラスラベルを対応付ける判別関数を学習せずに訓練データセットを暗記するような動作を取るため、怠惰学習（lazy leaner）の代表例として知られています。

以下の実装では、距離指標にユークリッド距離を用いて学習と予測を行っています。

実装

k-means

k-meansとは、教師無し学習であるクラスタリングアルゴリズムの中でもっともよく知られているアルゴリズムの1つです。実行にはクラスタの個数$k$を指定する必要があります。k-meansが最も効果的なのは球状または円状ののクラスタの識別です。

以下の実装では、k-meansの仕組みの説明も併せて行います。

実装

SVM

2種類のラベルの付いたデータを超平面で分割する超平面を学習により設定することで、新しく加わったデータを超平面を境界にして2種類のラベルのどちらかに分類するという教師学習モデルの1つです。

超平面と最も近いデータをサポートベクタと呼び、サポートベクタと超平面の距離をマージンと呼びます。データを学習するということは、マージンを最大化する超平面を更新していくことを意味します。

f:id:kazukiigeta:20210528081843j:plain — SVM概念図

実装

以下の3種類のSVMについて、数学的な説明とPythonによる実装を示します。

元のデータ空間において、線形分類可能で、データに重なりがない場合に利用できるハードマージンSVM
元のデータ空間において、線形分類可能不可能で、データに重なりがない場合に利用できるハードマージンSVM＋カーネル法
元のデータ空間において、線形分類可能で、データに重なりがある場合に利用できるソフトマージンSVM

未学習/過学習

主に教師あり学習を想定して、未学習および過学習それぞれについての対策についての概要を示します。

	未学習 (Underfitting)	過学習 (Overfitting)
対策1	訓練時間を延ばす	訓練時間を短くする
対策2	表現力の高いモデルを採用する	不要な既定関数（変数）を削除し表現力を抑制する
対策3	正則化のペナルティを小さくする	正則化法を利用して表現力を抑制する
対策4		訓練データを増やす

参考文献

機械学習のエッセンス
- 機械学習の数学的な理解に必要となる「数学」自体の解説から「機械学習」の解説までがこれ1冊で済んでしまうという初心者にとてもありがたい1冊です。E資格講座の解説だけでは理解できなかった部分をこの本にずいぶんと助けられました。
Python機械学習プログラミング達人データサイエンティストによる理論と実践
- 理論と合わせてPythonコードが豊富に掲載されているため、機械学習モデルを自分で実装してみるにはうってつけです。

最後に

今回は機械学習の基礎的なアルゴリズムについての理論の理解にフォーカスして記事をまとめてみました。実装も載せていますが、あくまでメイントピックは理論の学習としています。

理解に時間がかかる部分は、だいたいシグマで総和を取る表記と行列演算の書き換え部分だということが自分の中で見えてきました。その部分だけに注目した記事を書いてみても良いかと思っています。

今回の記事はここまで。Kazuki Igetaでした😃

2021-05-13

nteractによってコード1行でデータをインタラクティブに可視化

データサイエンス実装

nteractというデータ可視化ツールを使って、実際にTitanicのデータを描画してみました。

コードを1行だけで、Jupyter notebookの機能にインタラクティブなデータ可視化が追加されるため便利に使えそうな所感です。

インストール方法、利用時に感じた便利さと、注意点も含めて記事を書いていきます😃

環境
インストール
実際に使ってみる
nteract利用の注意点
最後に

環境

Windows10
Miniconda

インストール

① Anaconda Prompt (Miniconda3)を開きます。

② 以下のコマンドを実行してnteractをインストールします。

conda install -c conda-forge nteract_on_jupyter

③ 以下のコマンドを実行してnteractを起動します。

jupyter nteract

④ ブラウザでnteractが立ち上がるので、Start a new notebookにてNotebookを作成します。

実際に使ってみる

定番のTitanicのデータセットをつかって、データをインタラクティブに表示してみましょう。

以下にサンプルPythonコードを置きます。 pd.options.display.html.table_schema = Trueを入れないとインタラクティブな表示にはならないので注意です。

import pandas as pd


pd.options.display.html.table_schema = True
df = pd.read_csv('./train.csv')

上記Pythonスクリプトを実行してみると、以下のGif動画で示した通り、セル幅を変更したりカラムを昇順・降順に並び替えたりできます。

Show Filtersボタンから各カラムにフィルタをかけることもできます。PandasのDataFrameをExcelのように扱えるので便利ですね。

さらに、テーブル右のツールバーから表示形式を選択することで各種のグラフでデータを表示することもできます。

上記Gif動画の様に、MetirxにSurvivedを選択してバイオリンプロットみると、男性より女性の方が生存者の割合が多いことが瞬時に判断できますね。

nteract利用の注意点

注意点1: サイズの大きいデータでは可視化に時間がかかる

サイズの大きいデータに時間がかかるのは当たり前のことなんですけどね。

私の環境では、29.4MBのCSVを表示するのに1分16秒、テーブル表示からバイオリンプロット表示に切り替えるのに26秒が必要でした。

各種ボタンのクリック1つで簡単にインタラクティブにテーブルやグラフの表示方法を変更できるため、ギャップで表示までの待ち時間が長く感じるということだと思っています。

注意点2: テーブルやグラフ上で表示されるカラム数・行数は、通常のPandas DataFrameの表示上限に依存する

こちらも当たり前のことではあるんですけど、インタラクティブな可視化にばかり目が行っているとしばらく気づかないこともあります（私のことです😂）

以下のコードでカラム数および行数の表示上限を適切な値に設定してあげる必要があるということですね。

pd.set_option('display.max_rows', None)
pd.set_option('display.max_columns', None)

注意点3: Notebookを開いた際に画面上部のツールバーのみが表示されてセルが表示されないことがある

nteractを実行しているコマンドプロンプトをマウス/キーボード操作することで解消されました。

ただし、この記事を書くために再現試験を行ったところ事象が再発しないため、皆さんの環境でも発生し得るのか私の環境依存なのかが分からない状況です...

最後に

操作が簡単な分だけギャップとして表示変更の待ち時間を長く感じてしまいますが、データの性質を理解するのに便利なことは間違いないので継続して使っていこうと思います。

今回の記事はここまで。Kazuki Igetaでした😃

2021-04-22

機械学習で必要となる応用数学の基礎

応用数学統計学

今回は機械学習・データサイエンスに必要な応用数学について基礎的で重要な部分のまとめを行ったので紹介していきます😃

E資格の認定プログラムであるラビットチャレンジの講義や、プログラミングのための線形代数、現場ですぐ使える時系列データ分析、言語処理のための機械学習入門といった書籍の内容を解釈に以下にまとめていきます。

目次の中で★のついた項目は、私の中で特に重要な学びを得られた部分なので重点的に説明を行います。

線形代数
確率・統計
情報理論
最後に

線形代数

★固有値・固有ベクトル

以下の式(1)を満たす数λとベクトルxを、それぞれ固有値、固有ベクトルと呼びます。

$\displaystyle{ A\boldsymbol{x} = \lambda \boldsymbol{x} \ \ \ where \ \boldsymbol{x} \neq \boldsymbol{0} \tag{1} }$

具体例として、以下の行列Aの固有値および固有ベクトルを求めてみましょう。

具体例1: 固有値および固有ベクトルの算出

$\displaystyle{ A = \begin{pmatrix}1&4\\2&3\end{pmatrix} \\ }$

まずは、式(1)を変形して固有値を求めます。n×nの正方行列の固有値はn個ありますが、同じ値の重複（重解）があり得るため実際にはn種類の値を取ります。

$\displaystyle{ (A - \lambda) \boldsymbol{x} = \boldsymbol{0} \tag{2}\\ }$

$\displaystyle{ \begin{pmatrix}1-\lambda&4\\2&3-\lambda\end{pmatrix} \begin{pmatrix}x_1\\x_2\end{pmatrix} = \boldsymbol{0} \\ \begin{vmatrix}1-\lambda&4\\2&3-\lambda\end{vmatrix} = \boldsymbol{0} \ \ \because 式(1)より \, \boldsymbol{x} \neq \boldsymbol{0} \\ (1 - \lambda)(3 - \lambda) - 8 \\ (\lambda - 5)(\lambda +1) = \boldsymbol{0} \\ \therefore \lambda = -1, 5 }$

次に、求めた固有値から固有ベクトルを求めます。

$\displaystyle{ \lambda = -1 \ のとき\\ \begin{pmatrix}1&4\\2&3\end{pmatrix} \begin{pmatrix}x_1\\x_2\end{pmatrix} = -1 \begin{pmatrix}x_1\\x_2\end{pmatrix} \\ x_1 = -2 x_2 \\ \boldsymbol{x} = \begin{pmatrix}-2\\1\end{pmatrix} \\ \therefore \, \lambda = -1 のとき \, \boldsymbol{x} = \begin{pmatrix}-2\\1\end{pmatrix} \, の定数倍 }$

$\displaystyle{ \lambda = 5 \ のとき\\ \begin{pmatrix}1&4\\2&3\end{pmatrix} \begin{pmatrix}x_1\\x_2\end{pmatrix} = 5 \begin{pmatrix}x_1\\x_2\end{pmatrix} \\ x_1 = x_2 \\ \boldsymbol{x} = \begin{pmatrix}1\\1\end{pmatrix} \\ \therefore \, \lambda = 5 のとき \, \boldsymbol{x} = \begin{pmatrix}1\\1\end{pmatrix} \, の定数倍 }$

幾何学的な意味から固有値および固有ベクトルを説明すると、行列Aを固有ベクトルに掛けても伸縮が起きるだけでその方向は変化が起きません。この伸縮率が固有値となります。

上記画像はプログラミングのための線形代数・確率統計非公式サポートページより

次に、固有値および固有ベクトルがどんな場面で利用されているかについて説明していきます。

固有値および固有ベクトルが利用される場面

固有値および固有ベクトルは、行列の対角化を行う際に用いられます。そして対角化は、自己回帰モデルにてよく用いられています。自己回帰モデルとは、以下のようなモデルを意味します。

離散時間の例: 今日のξ(t)は、昨日のξ(t-1)、一昨日のξ(t-2)、一昨昨日のξ(t-3)と、今日のu(t)から次のように決まる。

$\displaystyle{ \xi(t) = -0.5 \xi(t-1) +0.34 \xi(t-2) + 0.08\xi(t-3) + 2u(t) \tag{3} \\ 初期条件 \, \xi(0) = 0.78, \, \xi(-1) = 0.8, \, \xi(-2) = 1.5 }$

$\displaystyle{ \boldsymbol{x}(t) = \begin{pmatrix}\xi(t)\\\xi(t-1)\\\xi(t-2)\end{pmatrix} \ とおき、u(t) = 0とすれば、以下の様に式(3)を行列で表現することができます。\\ }$

$\displaystyle{ \boldsymbol{x}(t) = \begin{pmatrix}-0.5&0.34&0.08\\1&0&0\\0&1&0\end{pmatrix} \boldsymbol{x}(t-1), \ \boldsymbol{x}(0) = \begin{pmatrix}0.78\\0.8\\1.5\end{pmatrix} \tag{4}\\ }$

これを一般化すると、以下の式(5)が得られます。

$\displaystyle{ \boldsymbol{x}(t) = A \boldsymbol{x}(t-1) \tag{5} }$

Aが対角行列である場合には、以下の様にAのt乗とx(0)で表すことができます。このとき、a, b, cいずれかの絶対値が1を超える場合にはt→∞ではx(t)が吹っ飛んで発散してしまうという判断を下すことができます。

$\displaystyle{ \boldsymbol{x}(t) = \begin{pmatrix}a&0&0\\0&b&0\\0&0&c\end{pmatrix} ^ t \boldsymbol{x}(0) \tag{6} }$

一方、Aが対角行列でない場合には、上記のように単純にt→∞のときにx(t)が発散するか判断することが出来ません。これを可能とするために行われるのが行列の対角化です。以下の具体例2では対角化の手法の1つである固有値分解を使った対角化を説明していきます。

具体例2: 固有値および固有ベクトルを使った固有値分解

ここから、式(4)の行列について、固有値および固有ベクトルを用いて行列を固有値分解してみようと思います。固有値分解には以下の式(7)*1を用います。

$\displaystyle{ \boldsymbol{x}(t) = P \Lambda^t P^{-1} \boldsymbol{x}(0) \tag{7} }$

まずは固有値および固有ベクトルを求めます。

$\displaystyle{ A = \begin{pmatrix}-0.5&0.34&0.08\\1&0&0\\0&1&0\end{pmatrix} \\ \lambda = -0.8 \, のとき \, 固有ベクトル \, \boldsymbol{p} = \begin{pmatrix}0.447\\-0.559\\0.698\end{pmatrix} \\ \lambda = 0.5 \, のとき \, 固有ベクトル \, \boldsymbol{p} = \begin{pmatrix}0.218\\0.436\\0.873\end{pmatrix} \\ \lambda = -0.2 \, のとき \, 固有ベクトル \, \boldsymbol{p} = \begin{pmatrix}-0.039\\0.196\\-0.980\end{pmatrix} \\ }$

$\displaystyle{ P = \begin{pmatrix}0.44703900498169&0.21821789023599&-0.039193090083481\\-0.55879875622711&0.43643578047199&0.1959654504174\\0.69849844528389&0.87287156094397&-0.97982725208702\end{pmatrix} \\ P^{-1} = \begin{pmatrix}1.8354389916075&-0.5506316974822&-0.18354389916075\\1.2589493667461&1.2589493667461&0.20143189867937\\2.4299715851758&0.72899147555276&-0.97198863407034\end{pmatrix} \\ \Lambda = \begin{pmatrix}-0.8&0&0\\0&0.5&0\\0&0&-0.2\end{pmatrix} \ \ }$

$\displaystyle{ \boldsymbol{x}(t) = \begin{pmatrix}0.44703900498169&0.21821789023599&-0.039193090083481\\-0.55879875622711&0.43643578047199&0.1959654504174\\0.69849844528389&0.87287156094397&-0.97982725208702\end{pmatrix} \begin{pmatrix}-0.8&0&0\\0&0.5&0\\0&0&-0.2\end{pmatrix} ^ t \begin{pmatrix}1.8354389916075&-0.5506316974822&-0.18354389916075\\1.2589493667461&1.2589493667461&0.20143189867937\\2.4299715851758&0.72899147555276&-0.97198863407034\end{pmatrix} \boldsymbol{x}(0) \tag{8} }$

桁数が大きくて見づらくなってしまいましたが、Pythonなどで計算するときは気にする必要がないので、ここでも気にせずにいきます。さて、以上の式(8)にて、離散時間の例で作成した自己回帰モデルをtの値毎に計算できるようになりました。

t乗が行列Λにのみ掛かっていることから、対角行列の場合、t→∞のときにx(t)が発散するかどうかはΛの要素の絶対値が1を超えるかどうかで判断されるということが分かるかと思います。今回の例でいうと絶対値が1を超える要素がないため、発散しないという結論が得られます。これは、期待値E[x(t)]がtによらず一定な、定常性を持つ時系列ということもできます。

特異値分解

固有値分解の便利さは前述したとおりですが、では、正方行列以外は対角化することはできないのでしょうか？正方行列でない行列を固有値分解するための手法が以下の特異値分解です。

$\displaystyle{ M \boldsymbol{v} = \sigma \boldsymbol{u} \tag{9} }$

$\displaystyle{ M^\mathrm{T} \boldsymbol{u} = \sigma \boldsymbol{v} \tag{10} }$

$\displaystyle{ 式(9), (10)が成立する単位ベクトル \, \boldsymbol{v}, \, \boldsymbol{u} \,が存在するとき、 \\ M = USV^\mathrm{T} \tag{11} }$

※ベクトルuおよびvを単位ベクトルとすることで、それぞれのベクトルの集まりである行列UおよびVが直行行列となるため、大きさ1となる単位ベクトルという条件が置かれています。

$\displaystyle{ M V = US \ \because \, 式(9) \\ M^\mathrm{T} U = V S^\mathrm{T} \ \because \, 式(10) \\ where \ V, \, U, \, S \,はそれぞれ\boldsymbol{v}, \, \boldsymbol{u}, \, \boldsymbol{\sigma} \,を列に集めた行列 \\ }$

$\displaystyle{ M = U S V^\mathrm{T} \\ M^\mathrm{T} = V S^\mathrm{T} U^\mathrm{T} \\ }$

$\displaystyle{ M M^\mathrm{T} = U S V^\mathrm{T} V S^\mathrm{T} U^\mathrm{T} = U S S^\mathrm{T} U^\mathrm{T} \tag{12} }$

つまり、式(12)のように、長方行列Mとその転置M^Tの積を固有値分解すれば、その左特異ベクトルUと特異値の2乗SS^Tが求められるということです。

具体例3: 簡単な特異値分解

$\displaystyle{ M = \begin{pmatrix}1&2&3\\3&2&1\end{pmatrix} \\ M M^\mathrm{T} = \begin{pmatrix}1&2&3\\3&2&1\end{pmatrix} \begin{pmatrix}1&3\\2&2\\3&1\end{pmatrix} = \begin{pmatrix}14&10\\14&10\end{pmatrix} \\ M M^\mathrm{T} \, を固有値分解して \\ M M^\mathrm{T} = \begin{pmatrix}14&10\\14&10\end{pmatrix} = \begin{pmatrix}1/\sqrt{3}&1/\sqrt{2}&1/\sqrt{6}\\1/\sqrt{3}&0&-2/\sqrt{6}\\1/\sqrt{3}&-1/\sqrt{2}&1/\sqrt{6}\end{pmatrix} \begin{pmatrix}24&0&0\\0&4&0\\0&0&0\end{pmatrix} \begin{pmatrix}1/\sqrt{3}&1/\sqrt{2}&1/\sqrt{6}\\1/\sqrt{3}&0&-2/\sqrt{6}\\1/\sqrt{3}&-1/\sqrt{2}&1/\sqrt{6}\end{pmatrix} ^ {-1} \\ M = \begin{pmatrix}1&2&3\\3&2&1\end{pmatrix} = \begin{pmatrix}1/\sqrt{2}&-1/\sqrt{2}\\1/\sqrt{2}&1/\sqrt{2}\end{pmatrix} \begin{pmatrix}2\sqrt{6}&0&0\\0&2&0\end{pmatrix} \begin{pmatrix}1/\sqrt{3}&1/\sqrt{3}&1/\sqrt{3}\\1/\sqrt{2}&0&-1/\sqrt{2}\\1/\sqrt{6}&-2/\sqrt{6}&1/\sqrt{6}\end{pmatrix} }$

参考文献

上述の線形代数の内容は、以下の書籍を参考としています。

プログラミングのための線形代数
- 「行列は写像だ」という本書決めフレーズが示すように、線形代数というものが意味の分からないただの計算としてとらえていた人に対して、実際には何のために用いられるものなのかをイメージとして持たせることに注力してくれている良書です。
現場ですぐ使える時系列データ分析
- 線形代数の考え方なしで、事前知識をほとんど必要としないシンプルかつ簡単な形で時系列データ分析を説明してくれる優れた入門書です。

確率・統計

確率には2つの異なる考え方が存在しています。

	頻度確立	ベイズ確率
概要	試行を繰り返すことで、結果は現象ごとに存在する真の確率に近づく。	いま手元にあるデータが、どのようなパラメータに基づく母集団（信念の度合い）から得られたのか推定する。
パラメータ	確率変数	データ
定数	データ	確率変数

ベイズ確率とは、「あなたがインフルエンザに罹患している確率は、40%です」のような信念の度合いには真の確率というものは存在せず、思考を繰り返すこともできないようなものを、いま手元にあるデータから推定することを意味しています。

条件付き確率

ある事象が与えられたもとで得られる確率のことを、条件付確率と呼びます。

例: 雨が降っている条件下で交通事故にあう確率

$\displaystyle{ P(Y=y | X=x) = \frac{P(Y=y, \,X=x)} {P(X=x)} \tag{13} }$

以下の様に、確率変数を省略し実現値のみで記載することも実際には頻繁にあります。

$\displaystyle{ P(y | x) = \frac{P(y, \,x)} {P(x)} }$

条件付確率は、同時確立を条件となる確率で割ってあげたものになっています。そのため以下の式(14)の通り、事象が互いに独立であれば、条件は確立に対して影響を与えません。

$\displaystyle{ P(y | x) = \frac{P(y, \,x)} {P(x)} = \frac{P(y)P(x)} {P(x)} = P(y) \tag{14} }$

ベイズの定理

ベイズの定理は、事前確率をもとに事後確率を計算することが出来るという非常に便利な定理です。

$\displaystyle{ P(y | x) = \frac{P(x|y)P(y)} {P(x)} \ \ \ where \ P(x) > 0 \tag{15} }$

P(y)は、事象xが起きる前の事象yの確率です。（事前確率） P(y|x)は、事象xが起きた後での、の事象yの確率です。（事後確率）

ベイズの定理により「飴玉をもらった子どもたちが笑顔になる確率」をもとに、「笑顔の子どもたちが飴玉をもらった確率」を求めるという具体例を以下に示します。

具体例4: ベイズの定理による確率の算出

$\displaystyle{ P(飴玉) = 1/4, \, P(笑顔|飴玉) = 1/2, \, P(笑顔) = 1/3 \\ \begin{eqnarray} P(飴玉|笑顔) &=& \frac{P(笑顔|飴玉)P(飴玉)} {P(笑顔)} \\ &=& 3/8 \\ \end{eqnarray} }$

期待値・分散

期待値

確率変数Xが離散型の場合

$\displaystyle{ E[X] = \sum_{i=1}^{n} {P(x) f(x)} \tag{16} }$

確率変数Xが連続型の場合

$\displaystyle{ E[X] = \int_{-\infty}^{\infty} {f(x) \, dx} \tag{17} }$

分散

確率変数Xが離散値の場合

$\displaystyle{ V[X] = \sum_{i=1}^{n} {(x_i - \mu)^2 p_i} \tag{18} }$

確率変数Xが連続値の場合

$\displaystyle{ V[X] = \int_{-\infty}^{\infty} {(x - \mu)^2 f(x) \, dx} \tag{19} }$

共分散

確率変数Xが離散値の場合

$\displaystyle{ Cov[X, \, Y] = \sum_{i=1}^n {(x_i- \overline{x})(y_i - \overline{y}) p_{XY}(x, \, y)} \tag{20} }$

確率変数Xが連続値の場合

$\displaystyle{ Cov[X, \, Y] = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} {(x - \mu_x)(y - \mu_y) f_{XY}(x, \, y) \, dxdy} \tag{21} }$

確率分布

確率分布とは、確率変数が取る値とその値を取る確率の対応の様子のことです。

ベルヌーイ分布

ベルヌーイ分布は、コインの裏か表のように二者択一の確率変数の分布です。ベルヌーイ分布の確率密度関数、期待値、分散はそれぞれ以下の様になります。

確率密度関数

$\displaystyle{ f(x)=p^x(1-p)^{1-x} \tag{22} }$

期待値

$\displaystyle{ E[X] = p \tag{23} }$

分散

$\displaystyle{ V[X] = p(1 - p) \tag{24} }$

なお、確率分布の期待値や分散といった特性は、確率母関数によって確率密度関数から導出することができます。統計検定準1級以上の試験範囲に含まれる内容です。

確率母関数による確率分布の特性の導出は以下の記事で説明を行っているので、興味のある方はそちらも読んでみてください。

kazukiigeta.com

情報理論

情報理論とは、情報を伝送するための理論的な基盤に関する学問のことです。

★自己情報量

以下の式(25)に自己情報量の定義を示します。自己情報量の単位は、対数の底が2のときbit、低が自然数eのときnatです。コンピュータの世界では2進数が用いられるため、bitの方が使われる場面が多いそうです。以降ではbitを用いて説明を行っていきます。

$\displaystyle{ I(x) = -\log_2{\left( P(x) \right)} \tag{25} }$

自己情報量とは、ある情報を表すことが出来るON/OFFの2通りの状態を持つスイッチの最小の数というように考えることが出来ます。例えば、1/2の確率で発生する事象を表すためにはスイッチが1つが必要となります。1/4の確率で発生する事象であればスイッチ2つ、1/8の確率であればスイッチ3つ、となります。つまり、確率が低い事象ほどその事象を表すために必要な情報量（スイッチの数）が増えることになります。

また、2つの情報が得られたとき、情報量はその2つの情報の足し算で表現することが出来ます。

具体例5: サイコロの出た目における情報量

サイコロは１～６までの6通りの目をそれぞれ1/6の確率で出すものとします。一般的な理想のサイコロですね。このサイコロを1回振った時の情報量を、以下の2つの情報をもとに算出してみます。

情報1: 出た目の数は4以上であった。
- 取り得る目は、4, 5, 6の3通りで、その確率P₁は1/2
情報2: 出た目の数は偶数であった。
- 取り得る目は、2, 4, 6の3通りで、その確率P₂は1/2

情報1と情報2の同時確立Pを求めると以下の様に1/4が得られます。

$\displaystyle{ P_1 = \frac{1}{2} \\ P_2 = \frac{1}{2} \\ 同時確立 \, P = P_1 \times P_2 = 1/4 }$

また、情報1と情報2を合わせた自己情報量Iを求めると以下の様に2が得られます。

$\displaystyle{ I_1 = -\log_2{\left( \frac{1}{2} \right)} \\ I_2 = -\log_2{\left( \frac{1}{2} \right)} \\ I = I_1 + I_2 = -\log_2{\left( \frac{1}{2} \right)} + \left( -\log_2{\left( \frac{1}{2} \right)} \right) = 1 + 1 = 2 }$

上記の自己情報量Iは、先ほど求めた同時確立Pから求めることもできます。

$\displaystyle{ I = -\log_2{\left( P \right)} = -\log_2{\left( P_1 \times P_2 \right)} = -\left( \log_2{\left( P_1 \right)} + \log_2{\left( P_2 \right)} \right) = 2 }$

シャノンエントロピー

シャノンエントロピーは、情報エントロピーとも呼ばれており確率あるいは確率分布/経験分布の「乱雑さ」を測るための尺度です。乱雑な状態とは、確率変数がどの値を取るか言い当てにくい状態を意味します。言い換えれば、確率分布が与えられたとき、その各値を取る確率が互いに大きく異なるとき乱雑さは小さく、シャノンエントロピーも小さいということになります。

以下に定義を記載します。自己情報量の期待値として定義されています。

$\displaystyle{ H(x) = E[I(x)] = -E[\log_2{\left( P(x) \right)}] = -\sum_{i=0}^{n}{\left( P(x_i) \log{\left( P(x_i) \right)} \right)} \tag{26} }$

★KLダイバージェンス

KLダイバージェンスは、カルバック・ライブラー情報量、KL情報量と呼ばれることもあります。同じ事象/確率変数における2つの確率分布P, Qに対して、それらの異なり具合を測るものです。

事前情報の確率Q(x)と、実験/観測によって新しく得られた情報の確率P(x)との珍しさの差や、新しく得られた情報の量を知ることができます。

例えば、サイコロの目という同じ確率変数においては、一般的な理想的なサイコロは全ての目が1/6の確率Q(x)で出る一様分布に従うという事前情報を持っており、手元のサイコロで実験を行ったところ得られた確率P(x)との差分を見るという場合などに用いられます。

$\displaystyle{ D_{KL}(P||Q) = \mathbb{E}_{x \sim P} [ \log_2{\frac{P(x)}{Q(x)}} ] = \mathbb{E}_{x~P} [ \log_2{P(x) - \log_2{Q(x)}} ] \tag{27} }$

KLダイバージェンスは実は、Q(x)の自己情報量からP(x)の自己情報量を差し引いたものをPで平均を取ったものとなっています。

$\displaystyle{ I\left( Q(x) \right) - I\left( P(x) \right) = \left( -\log_2{\left( Q(x) \right)} \right) - \left( -\log_2{\left( P(x) \right)} \right)= \log_2{\frac{P(x)}{Q(x)}} }$

交差エントロピー

KLダイバージェンスは、「Qについての自己情報量をPの分布で平均したもの」から「Pについての自己情報量をPの分布で平均したもの」を差し引いた差分として定義されていました。一方、交差エントロピーはQについての自己情報量をPの分布で平均したものを表しています。

$\displaystyle{ \begin{eqnarray} H(P, \, Q) &=& H(P) + D_{KL}(P||Q) \\ &=& -\mathbb{E}_{x \sim P} \log_2{Q(x)} \\ &=& -\sum_{x} {P(x) \log_2{Q(x)}} \tag{28} \end{eqnarray} }$

式(28)は、KLダイバージェンスの定義である式(27)から以下のように変形することで取り出すことが出来ます。

$\displaystyle{ \begin{eqnarray} D_{KL}(P||Q) &=& \sum_x {P(x) \left( -\log_2{\left( Q(x) \right)} \right) - \left( -\log_2{\left( P(x) \right)} \right)} \ \because 式(27) \\ &=& H(P, \, Q) - H(P) \end{eqnarray} }$

参考文献

上述の情報理論の内容は以下の書籍を参考にしています。

言語処理のための機械学習入門
- 数学的な予備知識は多少必要になるものの、応用数学が実際に機械学習の場面でどのように使われているかを理論として理解するための足掛かりとなる良書です。

最後に

今回の記事でまとめた応用数学の基礎を学んだことで、機械学習系の書籍を読んだ際に理解できる内容が増えてきました。良い学びを得られたのだと感じています。

次回は同様の形式で、機械学習の基礎についての記事を公開しますので興味があればそちらもぜひ読んでいただければと思います。

今回の記事はここまで。Kazuki Igetaでした😃

*1:プログラミングのための線形代数第4章に式の導出が記されています。

2021-04-04

データサイエンス界隈は教材が充実している

ポエム系

私は、データドリブンな考え方/課題解決方法をツールとして身に着けることが自分の専門性形成に必ず役立つと考え、サイバーセキュリティの世界*1 からデータサイエンスの世界に足を踏み入れてきました。

そんな中で、応用数学や機械学習などの分野は学習教材や環境が異様に充実していることを感じました。

これは、サイバーセキュリティの様に利益を攻撃者に奪われることから守るという世界から、利益を稼ぐビジネスの主戦場に足を踏み入れたことによるギャップからくるものだろうと思っています。

f:id:kazukiigeta:20210404165350j:plain

サイバーセキュリティの入門書の良書は沢山あります。

サイバーセキュリティ教材の対応レベルが低いということはなく、データサイエンス界隈の教材の対応レベルが幅広いのだろうと思っています。

最近は本屋さんに並ぶサイバーセキュリティの書籍もかなり増えてきており、教材と実戦の間の距離もどんどん縮まってきていることと思います。

それでも私は、サイバーセキュリティの書籍や資格による学習よりは、新しいマルウェアの解析を行うことや、マルウェアの解析妨害テクニックを解読し自分のバイナリとしてそのテクニックを実装してみることで得られる知見の方が自らの技術力向上には役に立つと考えていました。*2

しかし、データサイエンスの様に数学や統計学等の学問との結びつきが強く、積極的に利益を生み出すことを狙う領域では教材の充実度がとても高く、それらを活用することで体系的に学び先駆者を追いかけることで効率よく自身を高めることが出来るはずだと感じています。

今回の記事はここまで。Kazuki Igetaでした😃

*1:binarygenes.com

*2:Kernelやバイナリ等の技術領域にフォーカスした書籍から学ぶのは非常に有効と思います

2021-03-31

確率母関数で確率分布の特性が求められる

統計学

f:id:kazukiigeta:20210331112939p:plain ベルヌーイ分布や、ポアソン分布、幾何分布などの確率分布の平均や分散といった特性を自分で算出することができるのを皆さんご存じですか？

私は、統計検定準1級の勉強中にそのことを知って、ちょっとした感動を覚えました。

今まで何となく暗記していたものを、ちゃんと自分で導出できるようになるのって嬉しいですよね😆

というわけで、今回は確率分布の特性を自分で算出することができる確率母関数についての記事を書きます。

確率母関数 (Probability generating function)とは

確率密度関数から平均、分散、歪度、尖度といった分布の特性を算出することができる関数です。

以下の式で定義されています。

式

$\displaystyle{ G(s) = E[s^{X}] = \sum_{x} s^x f(x) }$

中身は非常に単純で、確率変数s^xの期待値になっています。 f(x)は確率密度関数を意味しています。

条件

確率変数Xは整数値を取る。
1を含むある開区間のすべてのsに対して、右辺の和が収束すると仮定する。

確率母関数でベルヌーイ分布の期待値と分散を求めてみる

準備

まずは、確率母関数の式から期待値E[s^x]を求める式を導出します。

G(s)の導関数にs=1とおいたとき、G^'(1)はXの期待値を表します。

$\displaystyle{ G^{'}(s) = E[Xs^{X-1}] }$
$\displaystyle{ G^{'}(1) = E[X] }$

G(s)の2次導関数にs=1とおいたとき、G^''(1) + G^'(1)はX²の期待値を表します。

$\displaystyle{ G^{''}(s) = E[X(X-1)s^{X-2}] }$
$\displaystyle{ G^{''}(1) = E[X(X-1)] = E[X^2] - E[X] }$

したがって、G^''(1)とG^'(1)を使ってXの分散を求めることが出来ます。

$\displaystyle{ G^{''}(1) + G^{'}(1) + \{G^{'}(1)\}^2 = E[X^2] - \{E[X]\}^2 = V[X] }$

ベルヌーイ分布に適用

ここからは、確率母関数を用いる実例として、ベルヌーイ分布の期待値と分散を求めてみることにします。

確率母関数を利用するためには、分布の確率密度関数が必要となるため、以下に記載します。

ベルヌーイ分布の確率密度関数

$\displaystyle{ f(x)=p^x(1-p)^{1-x} }$

ベルヌーイ分布の確率母関数G(s)は、以下の様になります。

$\displaystyle{ G(s) = E[s^{X}] = \sum_{x} s^x f(x) = \sum_{x} s^x p^x(1-p)^{1-x} }$

ベルヌーイ分布の確率変数Xは0か1の2値のみを取り得る（x∈{0, 1}）ため、それぞれ代入して和を取ると以下の様になります。

$\displaystyle{ G(s) = \sum_{x∈\{0, 1\}} s^x p^x(1-p)^{1-x} = 1 - p + sp }$

以上より、次のように期待値E[X]と分散V[X]を求めることが出来ます。

$\displaystyle{ G^{'}(s) = p }$
$\displaystyle{ G^{''}(s) = 0 }$
$\displaystyle{ G^{'}(1) = p }$
$\displaystyle{ G^{''}(1) = 0 }$
$\displaystyle{ E[X] = G^{'}(1) = p }$
$\displaystyle{ V[X] = G^{''}(1) + G^{'}(1) + \{G^{'}(1)\}^2 = 0 + p - p^2 = p(1 - p) }$

補足

確率母関数は正の整数にのみ利用可能ですが、モーメント母関数を使えば連続確率変数で対しても同じように分布の特性を求めることができるようになります。

また、確率母関数はk階微分を行うとE[X(X-1)(X-2)...(X-k+1)]のようにk次階乗モーメントを容易に求められるという点でメリットがあるそうです。一方で、ただ期待値（1次モーメント）と分散（2次モーメント）を算出したいだけなら実はモーメント母関数を使った方が算出が簡単になります。

日本統計学会公式認定統計検定準1級対応統計学実践ワークブックには、確率母関数とモーメント母関数さらには特性関数なんてものまで紹介されていました。

https://www.amazon.co.jp/%E6%97%A5%E6%9C%AC%E7%B5%B1%E8%A8%88%E5%AD%A6%E4%BC%9A%E5%85%AC%E5%BC%8F%E8%AA%8D%E5%AE%9A-%E7%B5%B1%E8%A8%88%E6%A4%9C%E5%AE%9A%E6%BA%961%E7%B4%9A%E5%AF%BE%E5%BF%9C-%E7%B5%B1%E8%A8%88%E5%AD%A6%E5%AE%9F%E8%B7%B5%E3%83%AF%E3%83%BC%E3%82%AF%E3%83%96%E3%83%83%E3%82%AF-%E6%97%A5%E6%9C%AC%E7%B5%B1%E8%A8%88%E5%AD%A6%E4%BC%9A/dp/478060852X/ref=asc_df_478060852X/?tag=jpgo-22&linkCode=df0&hvadid=342414341173&hvpos=&hvnetw=g&hvrand=12426885836471452873&hvpone=&hvptwo=&hvqmt=&hvdev=c&hvdvcmdl=&hvlocint=&hvlocphy=1009332&hvtargid=pla-912476174347&psc=1&th=1&psc=1www.amazon.co.jp

最後に

データ分析や機械学習の手法など直接的にすぐ活用できる技術・知識だけでなく、それらを支える数学/統計の基礎知識についても少しずつ学んでいき、データサイエンティストとして成長していけたらと思います。

今回の記事はここまで。Kazuki Igetaでした😃

2021-03-22

データサイエンス界隈で覚えておくべき英単語集【2021/04/15更新】

英語

f:id:kazukiigeta:20210321214049p:plain

データサイエンス界隈でグローバルに活躍したいと思ったら、英語で論文も読む必要があるしコミュニケーションをとる必要も出てくるかと思います。

でも、数学用語とかその他テクニカルタームって簡単な意味の単語でも英語になった途端、まったく分からなくなることって多くないですか？

（私は中学生レベルの数学用語でも英語になると、どう表したらよいのか分からなくなることがあります...😂）

そこで、データサイエンス界隈でよく使われているけど自分が知らなかった英単語/フレーズを中心に、この記事にまとめていきます。

こだわりポイントとしては、意味と一緒に発音記号を載せておくことで発音と意味をセットで覚えられるようにしたところです。

まだまだ数は少ないですが、少しずつ更新していきます。

数学系

数学系

英語	意味	発音	例
convex	凸状の	kὰnvéks	convex function (凸関数)
concave	凸状の	kὰnkéɪv	concave function (凹関数)
intersection	積集合; 共通部分	ìnṭɚsékʃən	the intersection of the sets (２つの集合の積集合)
perpendicular	垂直の	p`ɚːpəndíkjʊlɚ	perpendicular line (垂線)
orthogonal	直交の	ɔːˈθɒɡənəl	orthogonal system (直交系)
cartesian	デカルトの	kɑɚtíːʒən	cartesian coordinate (デカルト座標)
euclidean	ユークリッドの	juːklídiən	euclidean distance (ユークリッド距離)
pythagorean	ピタゴラスの	pɪθ`ægəríːən	pythagorean theorem (ピタゴラスの定理)
magnitude	大きさ	mˈægnət(j)ùːd	the magnitude of the vectors (ベクトルの大きさ)
dimensionality	次元数	dɪˌmɛnʃʌˈnælʌti	the curse of dimensionality (次元の呪い)
logarithm	対数	lˈɔːgərìðm	logarithm of A to base B (Bを底とする対数A)
spurious	見かけ上の	spjˈʊ(ə)riəs	spurious correlation (疑似相関)
tangent	接線	tˈændʒənt	the slope of the tagent (接線の傾き)
derivative	導関数	dɪrívəṭɪv	partial derivative (偏導関数)
contour	輪郭	kάntʊɚ	contour plot (等高線図)
convergence	収束	kənvˈɚːdʒəns	repeat utill convergence (収束するまで繰り返し)
surjection	全射	sərˈdʒɛk ʃən	the function is a surjection (その関数は全射です)
injection	単射	ɪndʒékʃən	the composition of two injections is also an injection (二つの単射の組合せもまた一つの単射です)
bijection	全単射	baɪˈdʒɛk ʃən	a bijection is an invertible transformation (全単射は可逆な変換です)

この記事を更新しながらデータサイエンス界隈で必要な英語を身に着けていこうと思います。

今回の記事はここまで。Kazuki Igetaでした😃

2021-03-21

データサイエンス案件でプロトタイプを素早く作るにはipywidgetsが良さそう

データサイエンス実装

f:id:kazukiigeta:20210320091211p:plain

データサイエンスや機械学習の案件を進めるとき、皆さんはプロトタイプ開発に何を使ってますか？

PyQt5やTkinterなど、選択肢はいろいろあるかと思います。

私は、分析やモデル作成はJupyterlab上をやっているなら、そのままJupyterlab上でお客様に見せられるような簡易的なGUIが素早く作れたら楽だと思いました。

UI/UXを考えるのは、プロトタイプ作成⇔相手との認識合わせを繰り返してからでも良さそうだという考えです。

そこで、Jupyterlab上でインタラクティブな簡易GUIを作成できるipywidgetsを使ってみました。

今回は、ipywidgetsによるJupyterlab上での簡易GUI作成について紹介します😃

簡易GUI

今回のポイントは2点です。

Jupyterlab上の余計なコードを隠す（余計な情報で相手を混乱させないための配慮）

ipywidgetsで成果物の動作を見せる（実際に動かすことでお互いの認識をしっかりと合わせるため）

それぞれのやり方をこれから説明していきます。

1. Jupyterlab上の余計なコードを隠す

Jupyterlabのコードを表示/非表示できるボタン

JupyterlabのIssue上で紹介されていた方法を採用して、ボタンの1クリックでコードの表示/非表示を切り替えることが出来ました。

方法は簡単で、以下のコードをエディターの先頭の方のセルに記載するだけです。

from IPython.display import HTML HTML(''' <script src='//code.jquery.com/jquery-3.6.0.min.js'></script> <script> code_show=true; function code_toggle() { if (code_show){ $('div.input').hide(); $('div .jp-CodeCell .jp-Cell-inputWrapper').hide(); } else { $('div.input').show(); $('div .jp-CodeCell .jp-Cell-inputWrapper').show(); } code_show = !code_show } $( document ).ready(code_toggle); </script> <form action="javascript:code_toggle()"><input type="submit" value="Code on/off"></form>''')

なお、jqueryのバージョンはオリジナルのv3.3.1から現時点での最新v3.6.0へ書き換えてあります。

v3.5.0でXSSの脆弱性の修正が入っていました。

攻撃者がJupyterlabにアクセスできてしまう状況であればXSSを利用するまでもなく様々な攻撃を実施することができてしまうので、この修正自体が直接このプロトタイプ開発のセキュリティを向上することはなさそうです。

しかし、データ分析の案件では機密データを扱う場面も多くあるので、セキュリティの観点から動作上問題がなければ今回に限らず最新バージョンを使うことを心掛ける必要があると思っています🔐

2. ipywidgetsで成果物の動作を見せる

ipywidgetsによる簡易GUI表示

こんな感じに、Jupyterlab上で素早く簡易的なGUIを作成することができます。

GIF動画で表示したGUIのサンプルコードを以下に置いておきます。

import ipywidgets as widgets import pandas as pd import matplotlib.pyplot as plt from IPython.display import display class GUI(): def __init__(self): item_layout = widgets.Layout(margin='0 0 50px 0') self.output = widgets.Output() self.output.clear_output() self.fruits_nature = widgets.Output() self.fruits_nature.clear_output() self.button_run = widgets.Button(description='実行', button_style='danger') self.picked_fruits = widgets.SelectMultiple( options=['りんご', 'みかん', 'ぶどう'], value=['ぶどう'], description='果物', disabled=False, ) self.picked_clock = widgets.Dropdown( options=['09:00', '12:00', '15:00'], value='15:00', description='収穫時刻', disabled=False, ) self.picked_target_date = widgets.DatePicker( description='予測対象日', disabled=False, ) target_widgets = widgets.HBox( [self.picked_clock, self.picked_target_date], layout=item_layout) button_widgets = widgets.HBox( [self.button_run], layout=item_layout) tab = widgets.Tab([self.output, self.fruits_nature]) tab.set_title(0, '予測結果') tab.set_title(1, '果実特性') self.dashboard = widgets.VBox([ target_widgets, tab, button_widgets]) def _run(self, obj): self.output.clear_output() self.fruits_nature.clear_output() with self.fruits_nature: print('収穫時刻:', self.picked_clock.value) x = list(range(5)) y = [1, 5, 2, 7, 4] plt.plot(x, y) plt.show() with self.output: df_out = pd.DataFrame( { 'fruit': ['りんご', 'みかん', 'ぶどう'], 'clock': [self.picked_clock.value] * 3, 'yield': [54, 22, 19], }, index=[self.picked_target_date.value]*3) display(df_out) def display(self): display(self.dashboard) self.button_run.on_click(self._run) GUI().display()

ドロップダウンや複数選択、チェックボックスなど、ウィジェットの種類とその呼び出し方はipywidgetsの公式ドキュメントを確認すると良いです。

最後に

ipywidgetsは、他人に分析結果を見せるとき以外にも、自分の分析用に条件をいろいろ変えながらデータを眺めるときにも便利なのでこれからちゃんと使っていこうと思います。

今回の記事はここまで。Kazuki Igetaでした😃

#jupyterlab #データサイエンス #データサイエンティスト #機械学習 #Python

kazukiigeta 2021-03-21 16:43

もっと読む

コメントを書く