機械学習で必要となる応用数学の基礎 - マルウェア解析できるデータサイエンティストblog

今回は機械学習・データサイエンスに必要な応用数学について基礎的で重要な部分のまとめを行ったので紹介していきます😃

E資格の認定プログラムであるラビットチャレンジの講義や、プログラミングのための線形代数、現場ですぐ使える時系列データ分析、言語処理のための機械学習入門といった書籍の内容を解釈に以下にまとめていきます。

目次の中で★のついた項目は、私の中で特に重要な学びを得られた部分なので重点的に説明を行います。

線形代数
確率・統計
情報理論
最後に

線形代数

★固有値・固有ベクトル

以下の式(1)を満たす数λとベクトルxを、それぞれ固有値、固有ベクトルと呼びます。

$\displaystyle{ A\boldsymbol{x} = \lambda \boldsymbol{x} \ \ \ where \ \boldsymbol{x} \neq \boldsymbol{0} \tag{1} }$

具体例として、以下の行列Aの固有値および固有ベクトルを求めてみましょう。

具体例1: 固有値および固有ベクトルの算出

$\displaystyle{ A = \begin{pmatrix}1&4\\2&3\end{pmatrix} \\ }$

まずは、式(1)を変形して固有値を求めます。n×nの正方行列の固有値はn個ありますが、同じ値の重複（重解）があり得るため実際にはn種類の値を取ります。

$\displaystyle{ (A - \lambda) \boldsymbol{x} = \boldsymbol{0} \tag{2}\\ }$

$\displaystyle{ \begin{pmatrix}1-\lambda&4\\2&3-\lambda\end{pmatrix} \begin{pmatrix}x_1\\x_2\end{pmatrix} = \boldsymbol{0} \\ \begin{vmatrix}1-\lambda&4\\2&3-\lambda\end{vmatrix} = \boldsymbol{0} \ \ \because 式(1)より \, \boldsymbol{x} \neq \boldsymbol{0} \\ (1 - \lambda)(3 - \lambda) - 8 \\ (\lambda - 5)(\lambda +1) = \boldsymbol{0} \\ \therefore \lambda = -1, 5 }$

次に、求めた固有値から固有ベクトルを求めます。

$\displaystyle{ \lambda = -1 \ のとき\\ \begin{pmatrix}1&4\\2&3\end{pmatrix} \begin{pmatrix}x_1\\x_2\end{pmatrix} = -1 \begin{pmatrix}x_1\\x_2\end{pmatrix} \\ x_1 = -2 x_2 \\ \boldsymbol{x} = \begin{pmatrix}-2\\1\end{pmatrix} \\ \therefore \, \lambda = -1 のとき \, \boldsymbol{x} = \begin{pmatrix}-2\\1\end{pmatrix} \, の定数倍 }$

$\displaystyle{ \lambda = 5 \ のとき\\ \begin{pmatrix}1&4\\2&3\end{pmatrix} \begin{pmatrix}x_1\\x_2\end{pmatrix} = 5 \begin{pmatrix}x_1\\x_2\end{pmatrix} \\ x_1 = x_2 \\ \boldsymbol{x} = \begin{pmatrix}1\\1\end{pmatrix} \\ \therefore \, \lambda = 5 のとき \, \boldsymbol{x} = \begin{pmatrix}1\\1\end{pmatrix} \, の定数倍 }$

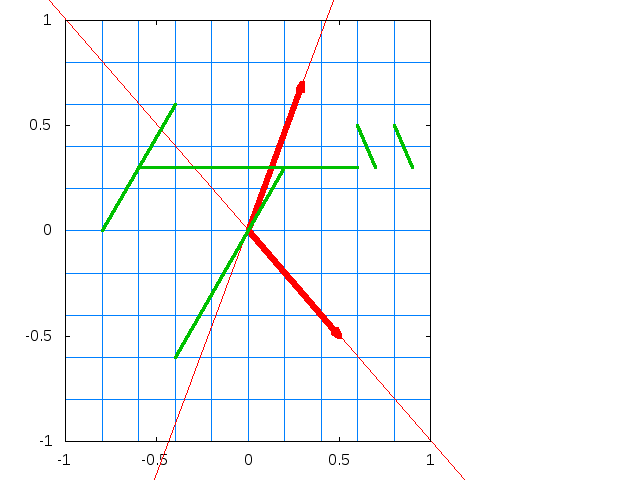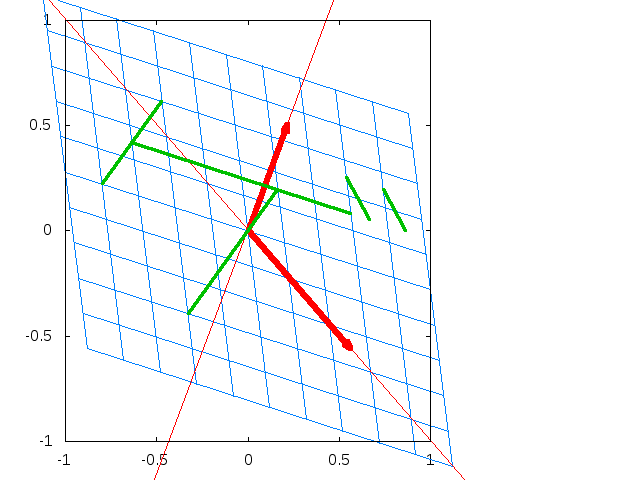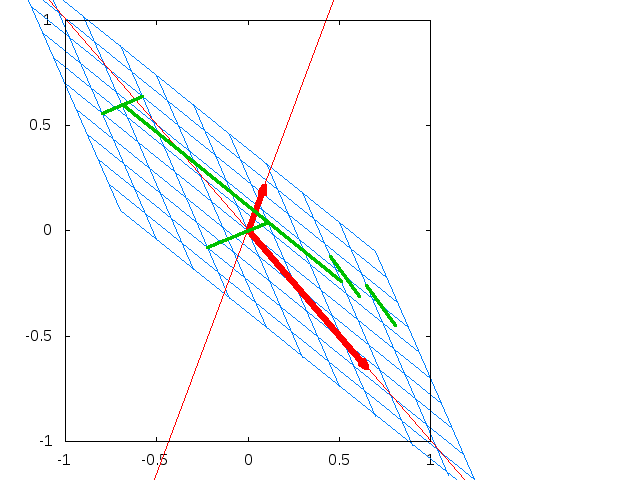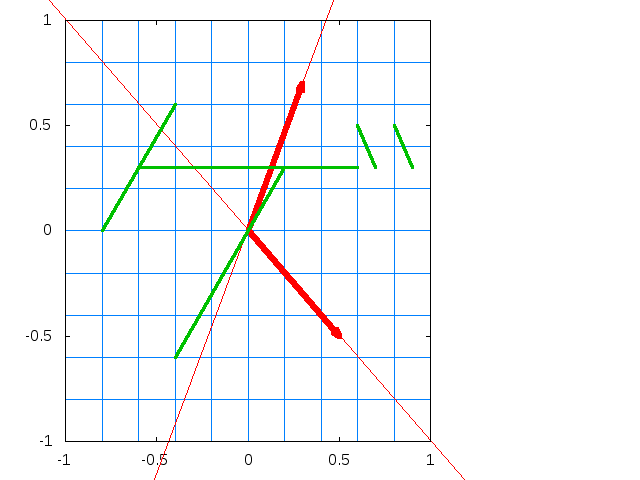
幾何学的な意味から固有値および固有ベクトルを説明すると、行列Aを固有ベクトルに掛けても伸縮が起きるだけでその方向は変化が起きません。この伸縮率が固有値となります。

上記画像はプログラミングのための線形代数・確率統計非公式サポートページより

次に、固有値および固有ベクトルがどんな場面で利用されているかについて説明していきます。

固有値および固有ベクトルが利用される場面

固有値および固有ベクトルは、行列の対角化を行う際に用いられます。そして対角化は、自己回帰モデルにてよく用いられています。自己回帰モデルとは、以下のようなモデルを意味します。

離散時間の例: 今日のξ(t)は、昨日のξ(t-1)、一昨日のξ(t-2)、一昨昨日のξ(t-3)と、今日のu(t)から次のように決まる。

$\displaystyle{ \xi(t) = -0.5 \xi(t-1) +0.34 \xi(t-2) + 0.08\xi(t-3) + 2u(t) \tag{3} \\ 初期条件 \, \xi(0) = 0.78, \, \xi(-1) = 0.8, \, \xi(-2) = 1.5 }$

$\displaystyle{ \boldsymbol{x}(t) = \begin{pmatrix}\xi(t)\\\xi(t-1)\\\xi(t-2)\end{pmatrix} \ とおき、u(t) = 0とすれば、以下の様に式(3)を行列で表現することができます。\\ }$

$\displaystyle{ \boldsymbol{x}(t) = \begin{pmatrix}-0.5&0.34&0.08\\1&0&0\\0&1&0\end{pmatrix} \boldsymbol{x}(t-1), \ \boldsymbol{x}(0) = \begin{pmatrix}0.78\\0.8\\1.5\end{pmatrix} \tag{4}\\ }$

これを一般化すると、以下の式(5)が得られます。

$\displaystyle{ \boldsymbol{x}(t) = A \boldsymbol{x}(t-1) \tag{5} }$

Aが対角行列である場合には、以下の様にAのt乗とx(0)で表すことができます。このとき、a, b, cいずれかの絶対値が1を超える場合にはt→∞ではx(t)が吹っ飛んで発散してしまうという判断を下すことができます。

$\displaystyle{ \boldsymbol{x}(t) = \begin{pmatrix}a&0&0\\0&b&0\\0&0&c\end{pmatrix} ^ t \boldsymbol{x}(0) \tag{6} }$

一方、Aが対角行列でない場合には、上記のように単純にt→∞のときにx(t)が発散するか判断することが出来ません。これを可能とするために行われるのが行列の対角化です。以下の具体例2では対角化の手法の1つである固有値分解を使った対角化を説明していきます。

具体例2: 固有値および固有ベクトルを使った固有値分解

ここから、式(4)の行列について、固有値および固有ベクトルを用いて行列を固有値分解してみようと思います。固有値分解には以下の式(7)*1を用います。

$\displaystyle{ \boldsymbol{x}(t) = P \Lambda^t P^{-1} \boldsymbol{x}(0) \tag{7} }$

まずは固有値および固有ベクトルを求めます。

$\displaystyle{ A = \begin{pmatrix}-0.5&0.34&0.08\\1&0&0\\0&1&0\end{pmatrix} \\ \lambda = -0.8 \, のとき \, 固有ベクトル \, \boldsymbol{p} = \begin{pmatrix}0.447\\-0.559\\0.698\end{pmatrix} \\ \lambda = 0.5 \, のとき \, 固有ベクトル \, \boldsymbol{p} = \begin{pmatrix}0.218\\0.436\\0.873\end{pmatrix} \\ \lambda = -0.2 \, のとき \, 固有ベクトル \, \boldsymbol{p} = \begin{pmatrix}-0.039\\0.196\\-0.980\end{pmatrix} \\ }$

$\displaystyle{ P = \begin{pmatrix}0.44703900498169&0.21821789023599&-0.039193090083481\\-0.55879875622711&0.43643578047199&0.1959654504174\\0.69849844528389&0.87287156094397&-0.97982725208702\end{pmatrix} \\ P^{-1} = \begin{pmatrix}1.8354389916075&-0.5506316974822&-0.18354389916075\\1.2589493667461&1.2589493667461&0.20143189867937\\2.4299715851758&0.72899147555276&-0.97198863407034\end{pmatrix} \\ \Lambda = \begin{pmatrix}-0.8&0&0\\0&0.5&0\\0&0&-0.2\end{pmatrix} \ \ }$

$\displaystyle{ \boldsymbol{x}(t) = \begin{pmatrix}0.44703900498169&0.21821789023599&-0.039193090083481\\-0.55879875622711&0.43643578047199&0.1959654504174\\0.69849844528389&0.87287156094397&-0.97982725208702\end{pmatrix} \begin{pmatrix}-0.8&0&0\\0&0.5&0\\0&0&-0.2\end{pmatrix} ^ t \begin{pmatrix}1.8354389916075&-0.5506316974822&-0.18354389916075\\1.2589493667461&1.2589493667461&0.20143189867937\\2.4299715851758&0.72899147555276&-0.97198863407034\end{pmatrix} \boldsymbol{x}(0) \tag{8} }$

桁数が大きくて見づらくなってしまいましたが、Pythonなどで計算するときは気にする必要がないので、ここでも気にせずにいきます。さて、以上の式(8)にて、離散時間の例で作成した自己回帰モデルをtの値毎に計算できるようになりました。

t乗が行列Λにのみ掛かっていることから、対角行列の場合、t→∞のときにx(t)が発散するかどうかはΛの要素の絶対値が1を超えるかどうかで判断されるということが分かるかと思います。今回の例でいうと絶対値が1を超える要素がないため、発散しないという結論が得られます。これは、期待値E[x(t)]がtによらず一定な、定常性を持つ時系列ということもできます。

特異値分解

固有値分解の便利さは前述したとおりですが、では、正方行列以外は対角化することはできないのでしょうか？正方行列でない行列を固有値分解するための手法が以下の特異値分解です。

$\displaystyle{ M \boldsymbol{v} = \sigma \boldsymbol{u} \tag{9} }$

$\displaystyle{ M^\mathrm{T} \boldsymbol{u} = \sigma \boldsymbol{v} \tag{10} }$

$\displaystyle{ 式(9), (10)が成立する単位ベクトル \, \boldsymbol{v}, \, \boldsymbol{u} \,が存在するとき、 \\ M = USV^\mathrm{T} \tag{11} }$

※ベクトルuおよびvを単位ベクトルとすることで、それぞれのベクトルの集まりである行列UおよびVが直行行列となるため、大きさ1となる単位ベクトルという条件が置かれています。

$\displaystyle{ M V = US \ \because \, 式(9) \\ M^\mathrm{T} U = V S^\mathrm{T} \ \because \, 式(10) \\ where \ V, \, U, \, S \,はそれぞれ\boldsymbol{v}, \, \boldsymbol{u}, \, \boldsymbol{\sigma} \,を列に集めた行列 \\ }$

$\displaystyle{ M = U S V^\mathrm{T} \\ M^\mathrm{T} = V S^\mathrm{T} U^\mathrm{T} \\ }$

$\displaystyle{ M M^\mathrm{T} = U S V^\mathrm{T} V S^\mathrm{T} U^\mathrm{T} = U S S^\mathrm{T} U^\mathrm{T} \tag{12} }$

つまり、式(12)のように、長方行列Mとその転置M^Tの積を固有値分解すれば、その左特異ベクトルUと特異値の2乗SS^Tが求められるということです。

具体例3: 簡単な特異値分解

$\displaystyle{ M = \begin{pmatrix}1&2&3\\3&2&1\end{pmatrix} \\ M M^\mathrm{T} = \begin{pmatrix}1&2&3\\3&2&1\end{pmatrix} \begin{pmatrix}1&3\\2&2\\3&1\end{pmatrix} = \begin{pmatrix}14&10\\14&10\end{pmatrix} \\ M M^\mathrm{T} \, を固有値分解して \\ M M^\mathrm{T} = \begin{pmatrix}14&10\\14&10\end{pmatrix} = \begin{pmatrix}1/\sqrt{3}&1/\sqrt{2}&1/\sqrt{6}\\1/\sqrt{3}&0&-2/\sqrt{6}\\1/\sqrt{3}&-1/\sqrt{2}&1/\sqrt{6}\end{pmatrix} \begin{pmatrix}24&0&0\\0&4&0\\0&0&0\end{pmatrix} \begin{pmatrix}1/\sqrt{3}&1/\sqrt{2}&1/\sqrt{6}\\1/\sqrt{3}&0&-2/\sqrt{6}\\1/\sqrt{3}&-1/\sqrt{2}&1/\sqrt{6}\end{pmatrix} ^ {-1} \\ M = \begin{pmatrix}1&2&3\\3&2&1\end{pmatrix} = \begin{pmatrix}1/\sqrt{2}&-1/\sqrt{2}\\1/\sqrt{2}&1/\sqrt{2}\end{pmatrix} \begin{pmatrix}2\sqrt{6}&0&0\\0&2&0\end{pmatrix} \begin{pmatrix}1/\sqrt{3}&1/\sqrt{3}&1/\sqrt{3}\\1/\sqrt{2}&0&-1/\sqrt{2}\\1/\sqrt{6}&-2/\sqrt{6}&1/\sqrt{6}\end{pmatrix} }$

参考文献

上述の線形代数の内容は、以下の書籍を参考としています。

プログラミングのための線形代数
- 「行列は写像だ」という本書決めフレーズが示すように、線形代数というものが意味の分からないただの計算としてとらえていた人に対して、実際には何のために用いられるものなのかをイメージとして持たせることに注力してくれている良書です。
現場ですぐ使える時系列データ分析
- 線形代数の考え方なしで、事前知識をほとんど必要としないシンプルかつ簡単な形で時系列データ分析を説明してくれる優れた入門書です。

確率・統計

確率には2つの異なる考え方が存在しています。

	頻度確立	ベイズ確率
概要	試行を繰り返すことで、結果は現象ごとに存在する真の確率に近づく。	いま手元にあるデータが、どのようなパラメータに基づく母集団（信念の度合い）から得られたのか推定する。
パラメータ	確率変数	データ
定数	データ	確率変数

ベイズ確率とは、「あなたがインフルエンザに罹患している確率は、40%です」のような信念の度合いには真の確率というものは存在せず、思考を繰り返すこともできないようなものを、いま手元にあるデータから推定することを意味しています。

条件付き確率

ある事象が与えられたもとで得られる確率のことを、条件付確率と呼びます。

例: 雨が降っている条件下で交通事故にあう確率

$\displaystyle{ P(Y=y | X=x) = \frac{P(Y=y, \,X=x)} {P(X=x)} \tag{13} }$

以下の様に、確率変数を省略し実現値のみで記載することも実際には頻繁にあります。

$\displaystyle{ P(y | x) = \frac{P(y, \,x)} {P(x)} }$

条件付確率は、同時確立を条件となる確率で割ってあげたものになっています。そのため以下の式(14)の通り、事象が互いに独立であれば、条件は確立に対して影響を与えません。

$\displaystyle{ P(y | x) = \frac{P(y, \,x)} {P(x)} = \frac{P(y)P(x)} {P(x)} = P(y) \tag{14} }$

ベイズの定理

ベイズの定理は、事前確率をもとに事後確率を計算することが出来るという非常に便利な定理です。

$\displaystyle{ P(y | x) = \frac{P(x|y)P(y)} {P(x)} \ \ \ where \ P(x) > 0 \tag{15} }$

P(y)は、事象xが起きる前の事象yの確率です。（事前確率） P(y|x)は、事象xが起きた後での、の事象yの確率です。（事後確率）

ベイズの定理により「飴玉をもらった子どもたちが笑顔になる確率」をもとに、「笑顔の子どもたちが飴玉をもらった確率」を求めるという具体例を以下に示します。

具体例4: ベイズの定理による確率の算出

$\displaystyle{ P(飴玉) = 1/4, \, P(笑顔|飴玉) = 1/2, \, P(笑顔) = 1/3 \\ \begin{eqnarray} P(飴玉|笑顔) &=& \frac{P(笑顔|飴玉)P(飴玉)} {P(笑顔)} \\ &=& 3/8 \\ \end{eqnarray} }$

期待値・分散

期待値

確率変数Xが離散型の場合

$\displaystyle{ E[X] = \sum_{i=1}^{n} {P(x) f(x)} \tag{16} }$

確率変数Xが連続型の場合

$\displaystyle{ E[X] = \int_{-\infty}^{\infty} {f(x) \, dx} \tag{17} }$

分散

確率変数Xが離散値の場合

$\displaystyle{ V[X] = \sum_{i=1}^{n} {(x_i - \mu)^2 p_i} \tag{18} }$

確率変数Xが連続値の場合

$\displaystyle{ V[X] = \int_{-\infty}^{\infty} {(x - \mu)^2 f(x) \, dx} \tag{19} }$

共分散

確率変数Xが離散値の場合

$\displaystyle{ Cov[X, \, Y] = \sum_{i=1}^n {(x_i- \overline{x})(y_i - \overline{y}) p_{XY}(x, \, y)} \tag{20} }$

確率変数Xが連続値の場合

$\displaystyle{ Cov[X, \, Y] = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} {(x - \mu_x)(y - \mu_y) f_{XY}(x, \, y) \, dxdy} \tag{21} }$

確率分布

確率分布とは、確率変数が取る値とその値を取る確率の対応の様子のことです。

ベルヌーイ分布

ベルヌーイ分布は、コインの裏か表のように二者択一の確率変数の分布です。ベルヌーイ分布の確率密度関数、期待値、分散はそれぞれ以下の様になります。

確率密度関数

$\displaystyle{ f(x)=p^x(1-p)^{1-x} \tag{22} }$

期待値

$\displaystyle{ E[X] = p \tag{23} }$

分散

$\displaystyle{ V[X] = p(1 - p) \tag{24} }$

なお、確率分布の期待値や分散といった特性は、確率母関数によって確率密度関数から導出することができます。統計検定準1級以上の試験範囲に含まれる内容です。

確率母関数による確率分布の特性の導出は以下の記事で説明を行っているので、興味のある方はそちらも読んでみてください。

kazukiigeta.com

情報理論

情報理論とは、情報を伝送するための理論的な基盤に関する学問のことです。

★自己情報量

以下の式(25)に自己情報量の定義を示します。自己情報量の単位は、対数の底が2のときbit、低が自然数eのときnatです。コンピュータの世界では2進数が用いられるため、bitの方が使われる場面が多いそうです。以降ではbitを用いて説明を行っていきます。

$\displaystyle{ I(x) = -\log_2{\left( P(x) \right)} \tag{25} }$

自己情報量とは、ある情報を表すことが出来るON/OFFの2通りの状態を持つスイッチの最小の数というように考えることが出来ます。例えば、1/2の確率で発生する事象を表すためにはスイッチが1つが必要となります。1/4の確率で発生する事象であればスイッチ2つ、1/8の確率であればスイッチ3つ、となります。つまり、確率が低い事象ほどその事象を表すために必要な情報量（スイッチの数）が増えることになります。

また、2つの情報が得られたとき、情報量はその2つの情報の足し算で表現することが出来ます。

具体例5: サイコロの出た目における情報量

サイコロは１～６までの6通りの目をそれぞれ1/6の確率で出すものとします。一般的な理想のサイコロですね。このサイコロを1回振った時の情報量を、以下の2つの情報をもとに算出してみます。

情報1: 出た目の数は4以上であった。
- 取り得る目は、4, 5, 6の3通りで、その確率P₁は1/2
情報2: 出た目の数は偶数であった。
- 取り得る目は、2, 4, 6の3通りで、その確率P₂は1/2

情報1と情報2の同時確立Pを求めると以下の様に1/4が得られます。

$\displaystyle{ P_1 = \frac{1}{2} \\ P_2 = \frac{1}{2} \\ 同時確立 \, P = P_1 \times P_2 = 1/4 }$

また、情報1と情報2を合わせた自己情報量Iを求めると以下の様に2が得られます。

$\displaystyle{ I_1 = -\log_2{\left( \frac{1}{2} \right)} \\ I_2 = -\log_2{\left( \frac{1}{2} \right)} \\ I = I_1 + I_2 = -\log_2{\left( \frac{1}{2} \right)} + \left( -\log_2{\left( \frac{1}{2} \right)} \right) = 1 + 1 = 2 }$

上記の自己情報量Iは、先ほど求めた同時確立Pから求めることもできます。

$\displaystyle{ I = -\log_2{\left( P \right)} = -\log_2{\left( P_1 \times P_2 \right)} = -\left( \log_2{\left( P_1 \right)} + \log_2{\left( P_2 \right)} \right) = 2 }$

シャノンエントロピー

シャノンエントロピーは、情報エントロピーとも呼ばれており確率あるいは確率分布/経験分布の「乱雑さ」を測るための尺度です。乱雑な状態とは、確率変数がどの値を取るか言い当てにくい状態を意味します。言い換えれば、確率分布が与えられたとき、その各値を取る確率が互いに大きく異なるとき乱雑さは小さく、シャノンエントロピーも小さいということになります。

以下に定義を記載します。自己情報量の期待値として定義されています。

$\displaystyle{ H(x) = E[I(x)] = -E[\log_2{\left( P(x) \right)}] = -\sum_{i=0}^{n}{\left( P(x_i) \log{\left( P(x_i) \right)} \right)} \tag{26} }$

★KLダイバージェンス

KLダイバージェンスは、カルバック・ライブラー情報量、KL情報量と呼ばれることもあります。同じ事象/確率変数における2つの確率分布P, Qに対して、それらの異なり具合を測るものです。

事前情報の確率Q(x)と、実験/観測によって新しく得られた情報の確率P(x)との珍しさの差や、新しく得られた情報の量を知ることができます。

例えば、サイコロの目という同じ確率変数においては、一般的な理想的なサイコロは全ての目が1/6の確率Q(x)で出る一様分布に従うという事前情報を持っており、手元のサイコロで実験を行ったところ得られた確率P(x)との差分を見るという場合などに用いられます。

$\displaystyle{ D_{KL}(P||Q) = \mathbb{E}_{x \sim P} [ \log_2{\frac{P(x)}{Q(x)}} ] = \mathbb{E}_{x~P} [ \log_2{P(x) - \log_2{Q(x)}} ] \tag{27} }$

KLダイバージェンスは実は、Q(x)の自己情報量からP(x)の自己情報量を差し引いたものをPで平均を取ったものとなっています。

$\displaystyle{ I\left( Q(x) \right) - I\left( P(x) \right) = \left( -\log_2{\left( Q(x) \right)} \right) - \left( -\log_2{\left( P(x) \right)} \right)= \log_2{\frac{P(x)}{Q(x)}} }$

交差エントロピー

KLダイバージェンスは、「Qについての自己情報量をPの分布で平均したもの」から「Pについての自己情報量をPの分布で平均したもの」を差し引いた差分として定義されていました。一方、交差エントロピーはQについての自己情報量をPの分布で平均したものを表しています。

$\displaystyle{ \begin{eqnarray} H(P, \, Q) &=& H(P) + D_{KL}(P||Q) \\ &=& -\mathbb{E}_{x \sim P} \log_2{Q(x)} \\ &=& -\sum_{x} {P(x) \log_2{Q(x)}} \tag{28} \end{eqnarray} }$

式(28)は、KLダイバージェンスの定義である式(27)から以下のように変形することで取り出すことが出来ます。

$\displaystyle{ \begin{eqnarray} D_{KL}(P||Q) &=& \sum_x {P(x) \left( -\log_2{\left( Q(x) \right)} \right) - \left( -\log_2{\left( P(x) \right)} \right)} \ \because 式(27) \\ &=& H(P, \, Q) - H(P) \end{eqnarray} }$